摘要:5. (1)设是各项均不为零的等差数列().且公差.若将此数列删去某一项得到的数列是等比数列: ①当时.求的数值,②求的所有可能值, (2)求证:对于一个给定的正整数.存在一个各项及公差都不为零的等差数列.其中任意三项都不能组成等比数列. [解析]:本小题考查等差数列.等比数列的综合应用. (1)①当n=4时, 中不可能删去首项或末项.否则等差数列中连续三项成等比数列.则推出d=0. 若删去.则.即化简得.得 若删去.则.即化简得.得 综上.得或. ②当n=5时, 中同样不可能删去.否则出现连续三项. 若删去.则.即化简得.因为.所以不能删去, 当n≥6时.不存在这样的等差数列.事实上.在数列中.由于不能删去首项或末项.若删去.则必有.这与矛盾,同样若删去也有.这与矛盾,若删去中任意一个.则必有.这与矛盾.(或者说:当n≥6时.无论删去哪一项.剩余的项中必有连续的三项) 综上所述.. (2)假设对于某个正整数n.存在一个公差为d的n项等差数列.其中()为任意三项成等比数列.则.即.化简得 (*) 由知.与同时为0或同时不为0 当与同时为0时.有与题设矛盾. 故与同时不为0.所以由(*)得 因为.且x.y.z为整数.所以上式右边为有理数.从而为有理数. 于是.对于任意的正整数.只要为无理数.相应的数列就是满足题意要求的数列. 例如n项数列1...--.满足要求.
网址:http://m.1010jiajiao.com/timu3_id_528014[举报]
(I)设 是各项均不为零的等差数列
是各项均不为零的等差数列 ,且公差
,且公差 ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当 时,求
时,求 的数值;②求
的数值;②求 的所有可能值;
的所有可能值;
(II)求证:对于一个给定的正整数 ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列 ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。
查看习题详情和答案>>
设![]() 是各项均不为零的等差数列
是各项均不为零的等差数列![]() ,且公差
,且公差![]() ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列。
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列。
(1)当n=4时,求![]() 的数值;w.w.w.k.s.5.u.c.o.m
的数值;w.w.w.k.s.5.u.c.o.m ![]()
(2)求n的所有可能值。
查看习题详情和答案>>(08年江苏卷)(I)设![]() 是各项均不为零的等差数列
是各项均不为零的等差数列![]() ,且公差
,且公差![]() ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
(1)① 当![]() 时,求
时,求![]() 的数值;②求
的数值;②求![]() 的所有可能值;
的所有可能值;
(2)求证:对于一个给定的正整数![]() ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列![]() ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。
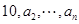 是各项均不为零的
是各项均不为零的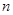 (
(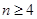 )项等差数列,且公差
)项等差数列,且公差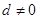 .
. ,且该数列前
,且该数列前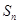 最大,求
最大,求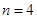 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;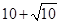 ,则数列
,则数列