5.(江西21)已知函数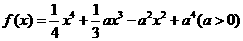
(1)求函数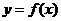 的单调区间;
的单调区间;
(2)若函数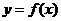 的图像与直线
的图像与直线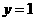 恰有两个交点,求
恰有两个交点,求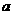 的取值范围.
的取值范围.
解:(1)因为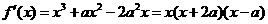
令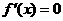 得
得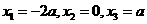
由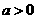 时,
时,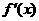 在
在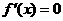 根的左右的符号如下表所示
根的左右的符号如下表所示
 |
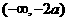 |
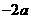 |
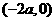 |
 |
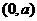 |
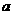 |
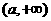 |
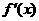 |
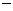 |
 |
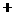 |
 |
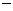 |
 |
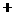 |
 |
 |
极小值 |
 |
极大值 |
 |
极小值 |
 |
所以 的递增区间为
的递增区间为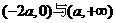
 的递减区间为
的递减区间为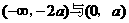
(2)由(1)得到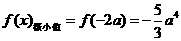 ,
,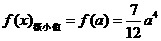
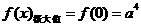
要使 的图像与直线
的图像与直线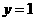 恰有两个交点,只要
恰有两个交点,只要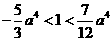 或
或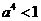 ,
,
即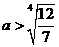 或
或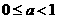 .
.
3.(福建21)(本小题满分12分)
已知函数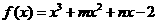 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数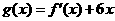 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:(1)由函数f(x)图象过点(-1,-6),得m-n=-3, ……①
由f(x)=x3+mx2+nx-2,得f′(x)=3x2+2mx+n,
则g(x)=f′(x)+6x=3x2+(2m+6)x+n;
而g(x)图象关于y轴对称,所以-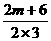 =0,所以m=-3,
=0,所以m=-3,
代入①得n=0.
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
|
X |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
 |
极大值 |
|
极小值 |
|
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,无极大值;当a=1或a≥3时,f(x)无极值.
2.(北京17)(本小题共13分)
已知函数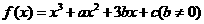 ,且
,且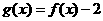 是奇函数.
是奇函数.
(Ⅰ)求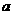 ,
,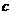 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
解:(Ⅰ)因为函数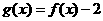 为奇函数,
为奇函数,
所以,对任意的 ,
,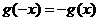 ,即
,即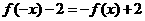 .
.
又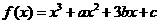
所以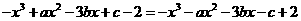 .
.
所以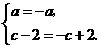
解得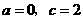 .
.
(Ⅱ)由(Ⅰ)得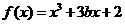 .
.
所以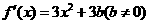 .
.
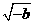
当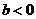 时,由
时,由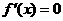 得
得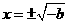 .
.
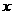 变化时,
变化时,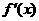 的变化情况如下表:
的变化情况如下表:
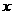 |
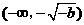 |
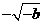 |
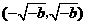 |
 |
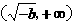 |
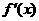 |
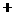 |
0 |
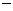 |
0 |
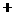 |
所以,当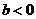 时,函数
时,函数 在
在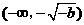 上单调递增,在
上单调递增,在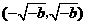 上单调递减,在
上单调递减,在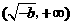 上单调递增.
上单调递增.
当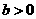 时,
时,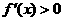 ,所以函数
,所以函数 在
在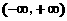 上单调递增.
上单调递增.
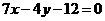 可化为
可化为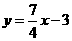 .
.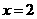 时,
时,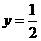 .···································································································· 2分
.···································································································· 2分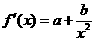 ,
,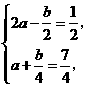 解得
解得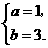
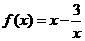 .········································································································· 6分
.········································································································· 6分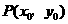 为曲线上任一点,由
为曲线上任一点,由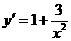 知曲线在点
知曲线在点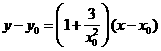 ,
,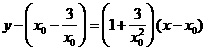 .
.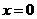 得
得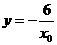 ,从而得切线与直线
,从而得切线与直线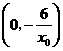 .
.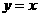 得
得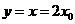 ,从而得切线与直线
,从而得切线与直线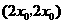 .·············· 10分
.·············· 10分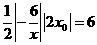 .
. . 12分
. 12分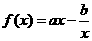 ,曲线
,曲线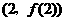 处的切线方程为
处的切线方程为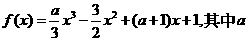 为实数。
为实数。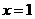 处取得极值,求
处取得极值,求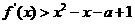 对任意
对任意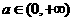 都成立,求实数
都成立,求实数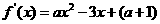 ,由于函数
,由于函数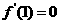
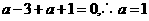
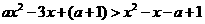 对任意
对任意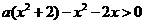 对任意
对任意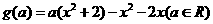 , 则对任意
, 则对任意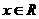 ,
,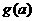 为单调递增函数
为单调递增函数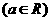
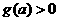 恒成立的充分必要条件是
恒成立的充分必要条件是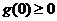
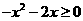 ,
,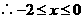
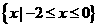
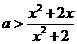 对任意
对任意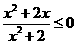
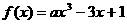 对于
对于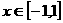 总有
总有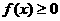 成立,则
成立,则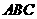 ,其中
,其中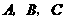 的坐标分别为
的坐标分别为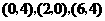 ,则
,则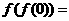 _________;2
_________;2 函数
函数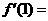 _________.
_________.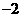
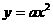 在点(1,
在点(1,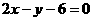 平行,则
平行,则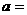 ( A )
( A )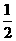 C.
C.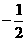 D.
D.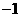
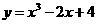 在点
在点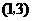 处的切线的倾斜角为( B )
处的切线的倾斜角为( B )