※设L1、L2是两条异面直线,其公垂向量为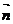 ,又C、D分别是L1、L2上任意一点,则
,又C、D分别是L1、L2上任意一点,则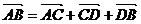
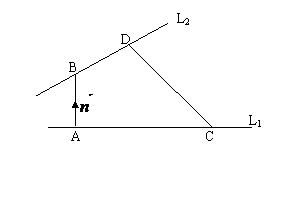
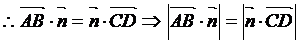
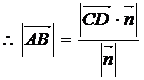
则L1、L2间的距离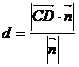
 [例5]已知正方体ABCD-A1B1C1D1的棱长为
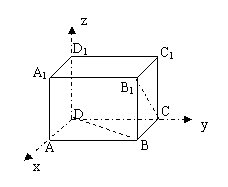
[例5]已知正方体ABCD-A1B1C1D1的棱长为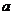 ,求异面直线BD与B1C的距离。
,求异面直线BD与B1C的距离。
解:如图,建立空间直角坐标系,则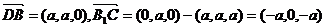
设DB与B1C的公垂向量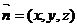
|
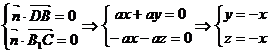
令x=-1,则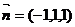 又
又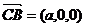 ,
,
所以异面直线BD与B1C的距离为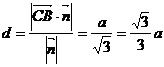 .
.
※直线与平面平行是直线与平面的法向量垂直问题,只取和直线平行的向量,验证该向量和平面的法向量的内积是否为零即可。
[例2]如图,四棱锥P-ABCD中PA⊥平面ABCD,PB与底面所成的角为450,底面ABCD为直角梯形,∠ABC=∠BAD=900,PA=BC=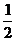 AD=
AD=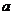
(1)求证:平面PAC⊥平面PCD(略)
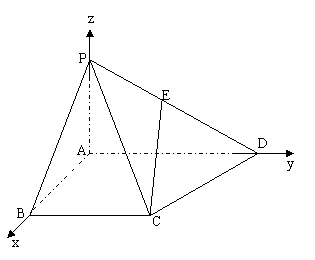 (2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。
(2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。
解:分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系(如图)
则P(0,0,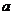 ),C(
),C(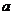 ,
,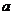 ,0),D(0,2
,0),D(0,2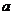 ,0)
,0)
设在棱PD上存在点E坐标为(0,y,z),
则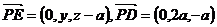
|
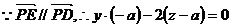
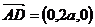 是平面PAB的法向量,又
是平面PAB的法向量,又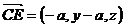
由CE//面PAB,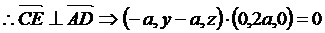
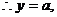 代入得
代入得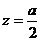
∴E是PD中点,
即存在点E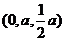 使得CE//面PAB。
使得CE//面PAB。
※直线与平面所成的角,是直线与平面的法向量所成的角(取锐角)的余角。
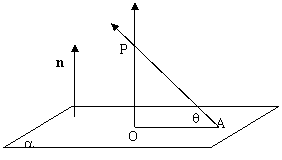
如图,已知PA为平面a的一条斜线,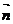 为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得
为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得
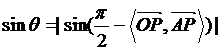

则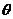 =
=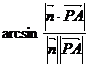
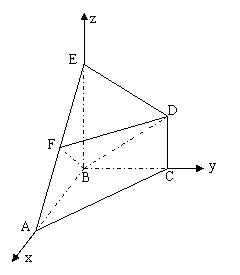 [例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
[例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
(1)证明:DF//平面ABC(略)
(2)求AB与平面BDF所成角的大小。
|
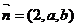
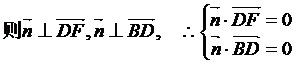 ,而
,而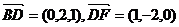
则得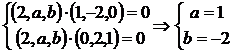 所以
所以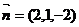
又设AB与平面BDF所成角为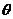 ,则法线
,则法线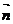 与
与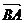 所成的角为
所成的角为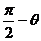

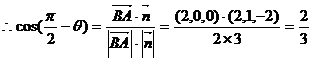
即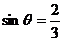 ,故AB与平面BDF所成的角为
,故AB与平面BDF所成的角为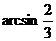
用法向量求解,不用作出AB与平面BDF所成的角,从而避开了作图的难度。
 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获 元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为
元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为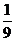 ,
,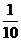 ,
,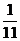 ,且各车是否发生事故相互独立,求一年内该单位在此保险中:
,且各车是否发生事故相互独立,求一年内该单位在此保险中: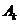 表示第
表示第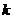 辆车在一年内发生此种事故,
辆车在一年内发生此种事故,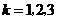 .由题意知
.由题意知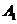 ,
,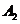 ,
,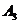 独立,
独立,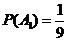 ,
,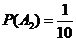 ,
,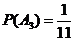 .
.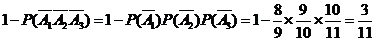 .
.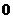 ,
,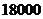 ,
,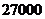 .
.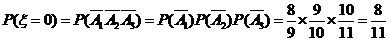 ,
,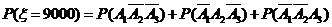
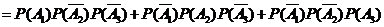
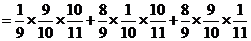
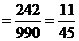 ,
,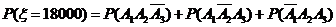
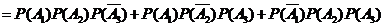
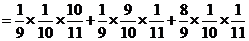
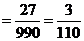 ,
,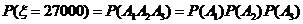
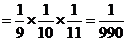 .
.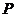
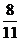
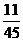

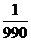
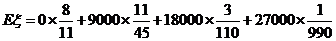
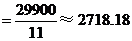 (元).
(元).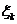 表示第
表示第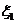 有分布列
有分布列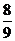
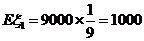 .
.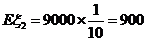 ,
,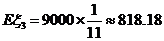 .
.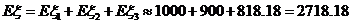 (元).
(元).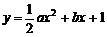 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是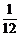 (B)
(B)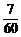 (C)
(C) (D)
(D)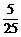
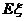 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
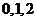
 ,
,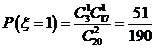 ,
,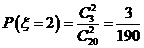
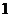
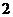

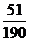
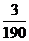
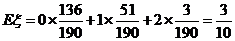
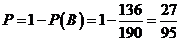
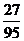
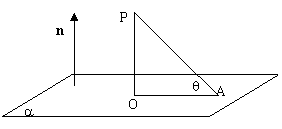 ※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为
※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为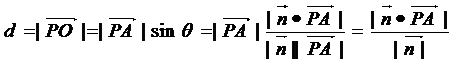
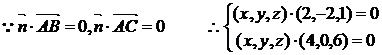
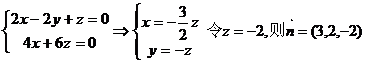
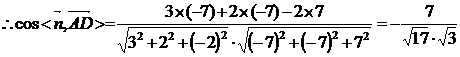
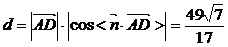
 ※如图在二面角
※如图在二面角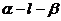 中
中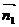 和
和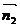 分别为
分别为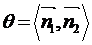 或
或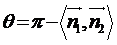 (依据两平面法向量的方向而定),但总有
(依据两平面法向量的方向而定),但总有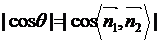 =
=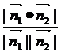 ,所以此时
,所以此时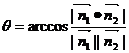 。
。 (ⅱ)若二面角
(ⅱ)若二面角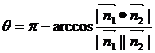
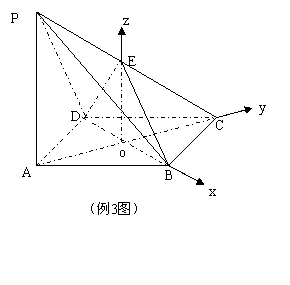 ∠BAD=600,AB=2,PA=4,E为PC的中点。
∠BAD=600,AB=2,PA=4,E为PC的中点。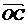 为平面EBD的法量,
为平面EBD的法量,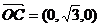 .
.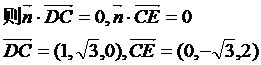
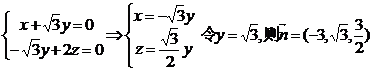
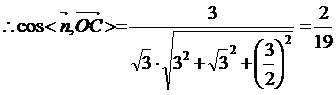 , 所以B-DE-C为
, 所以B-DE-C为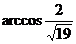 。
。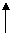 如右图,△ABC是一个正三角形,EC⊥平面ABC,
如右图,△ABC是一个正三角形,EC⊥平面ABC,

 BD∥CE,且CE=CA=2BD,M是EA的中点。
E
BD∥CE,且CE=CA=2BD,M是EA的中点。
E

 求证:(1)DE=DA;
M
D
求证:(1)DE=DA;
M
D 



 (2)平面BDM⊥平面ECA;
C
B
(2)平面BDM⊥平面ECA;
C
B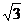 ,1,0),B(0,2,0),E(0,0,2),D(0,2,1),
,1,0),B(0,2,0),E(0,0,2),D(0,2,1),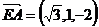 ,
,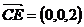 ,
,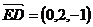 , 分别假设面CEA与面DEA的法向量是
, 分别假设面CEA与面DEA的法向量是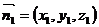 、
、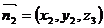 ,所以得
,所以得

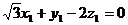
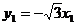
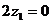
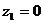
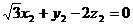
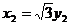
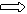
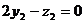

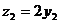
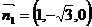 、
、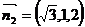 ,从而计算得
,从而计算得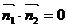 ,所以两个法向量相互垂直,两个平就相互垂直。
,所以两个法向量相互垂直,两个平就相互垂直。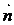 垂直于平面α,则向量
垂直于平面α,则向量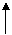 分析:作如图所示右手直角坐标系,
D
C
分析:作如图所示右手直角坐标系,
D
C











 B(1,1,1),D(0,0,1),
A1
B1
B(1,1,1),D(0,0,1),
A1
B1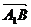 =(0,1,1),
=(0,1,1),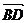 =(-1,-1,0),设平面A1BD有一法向量
=(-1,-1,0),设平面A1BD有一法向量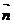 =(x,y,z),则
=(x,y,z),则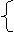
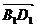 =(-1,-1,0),
=(-1,-1,0),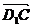 =(0,1,1),易知
=(0,1,1),易知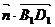 =
=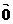 ,
, 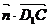 =
=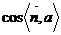 ,易知θ=
,易知θ=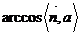 或者
或者
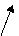 例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。
例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。


 过O作OF∥BC交CD于F,建立如图所
E
过O作OF∥BC交CD于F,建立如图所
E
 示右手直角坐标系,则O(0,0,0),
B
O
D
示右手直角坐标系,则O(0,0,0),
B
O
D



 E(0,
E(0,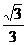 ,
,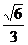 ),
), 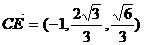 C
F
C
F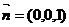 ,所以
,所以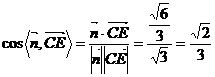 ,观察
,观察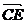 的方向,易知EC与平面BCD所成的角是
的方向,易知EC与平面BCD所成的角是