0 51866 51874 51880 51884 51890 51892 51896 51902 51904 51910 51916 51920 51922 51926 51932 51934 51940 51944 51946 51950 51952 51956 51958 51960 51961 51962 51964 51965 51966 51968 51970 51974 51976 51980 51982 51986 51992 51994 52000 52004 52006 52010 52016 52022 52024 52030 52034 52036 52042 52046 52052 52060 447348
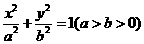 的左、右焦点分别为
的左、右焦点分别为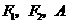 是椭圆上的一点,
是椭圆上的一点,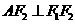 ,原点
,原点 到直线
到直线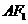 的距离为
的距离为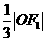 .
.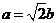 ;
;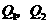 为椭圆上的两个动点,
为椭圆上的两个动点,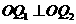 ,过原点
,过原点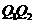 的垂线
的垂线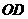 ,垂足为
,垂足为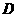 ,求点
,求点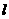 与双曲线
与双曲线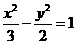 交于A,B两点,且
交于A,B两点,且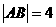 ,求直线的方程.
,求直线的方程.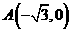 和
和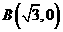 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线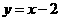 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.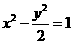 .
.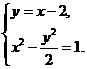 得
得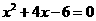 .
.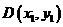 ,
,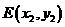 ,则
,则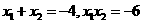 .
.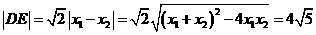 .
.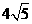 .
.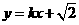 与椭圆
与椭圆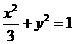 交于不同两点A和B,且
交于不同两点A和B,且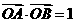 (其中O为坐标原点),求k的值.
(其中O为坐标原点),求k的值.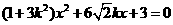 .
.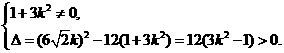 即
即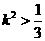 .
.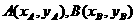 ,则
,则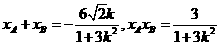 .
.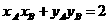 .
.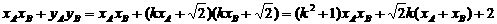
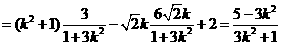 .
.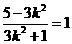 .解得
.解得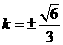 .故k的值为
.故k的值为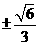 .
.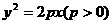 .过动点M(
.过动点M(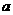 ,0)且斜率为1的直线
,0)且斜率为1的直线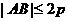 ,求a的取值范围.
,求a的取值范围.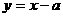 ,
,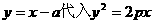 ,
,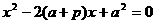 .
.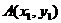 、
、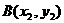 ,
,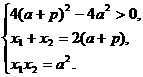
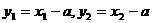 ,
,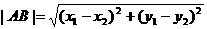
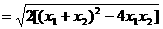
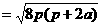 .
.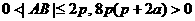 ,
,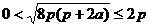 .
.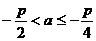 .
.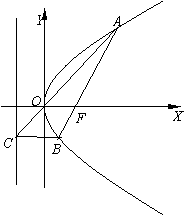 变式(2001年全国卷):设抛物线
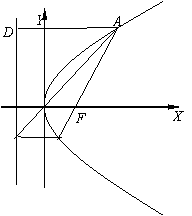
变式(2001年全国卷):设抛物线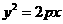 (
(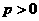 )的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
)的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.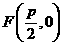 ,所以经过点F的直线AB的方程可设为
,所以经过点F的直线AB的方程可设为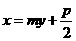 ,代人抛物线方程得
,代人抛物线方程得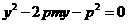 .
.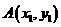 ,
,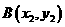 ,则
,则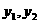 是该方程的两个根,所以
是该方程的两个根,所以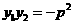 .
.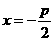 上,所以点C的坐标为
上,所以点C的坐标为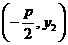 ,
, 故直线CO的斜率为
故直线CO的斜率为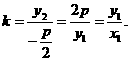
 也是直线OA的斜率,所以直线AC经过原点O.
也是直线OA的斜率,所以直线AC经过原点O.
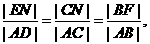
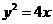 的焦点,且与抛物线相交于A,B两点,求线段AB的长.
的焦点,且与抛物线相交于A,B两点,求线段AB的长.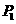 ,
,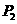 ,…,
,…,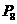 是抛物线
是抛物线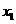 ,
,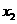 ,…,
,…,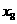 ,F是抛物线的焦点,若
,F是抛物线的焦点,若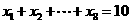 ,则
,则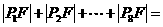 ___.
___.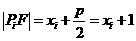 (
(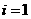 ,2,……,8),
,2,……,8),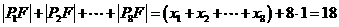 .
.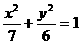 的右焦点,且椭圆上至少有21个不同的点
的右焦点,且椭圆上至少有21个不同的点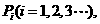 使
使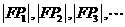 ,组成公差为d的等差数列,则d的取值范围为 .
,组成公差为d的等差数列,则d的取值范围为 .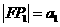 ,则
,则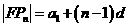 ,于是
,于是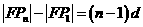 ,即
,即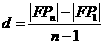 ,由于
,由于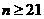 ,
,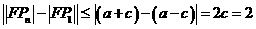 ,故
,故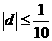 ,又
,又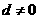 ,故
,故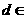
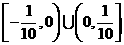 .
.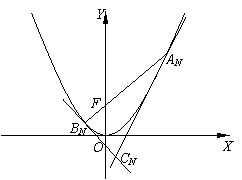 变式3(2006年重庆卷文):如图,对每个正整数
变式3(2006年重庆卷文):如图,对每个正整数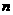 ,
,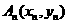 是抛物线
是抛物线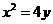 上的点,过焦点
上的点,过焦点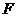 的直线
的直线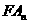 交抛物线于另一点
交抛物线于另一点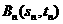 .
.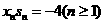 ;
;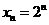 ,并记
,并记 为抛物线上分别以
为抛物线上分别以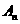 与
与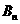 为切点的两条切线的交点.试证:
为切点的两条切线的交点.试证: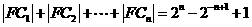 .
.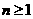 ,因为焦点
,因为焦点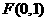 ,所以可设直线
,所以可设直线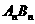 的方程为
的方程为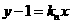 ,将它与抛物线方程
,将它与抛物线方程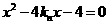 ,由一元二次方程根与系数的关系得
,由一元二次方程根与系数的关系得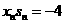 .
.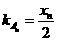 ,故
,故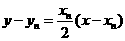 , ①
, ①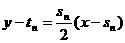 , ②
, ②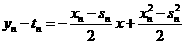 ,
,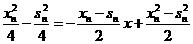 ,
, 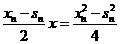 ,
,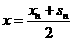 , ③
, ③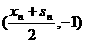 .
.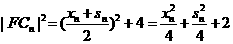
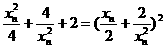 .从而
.从而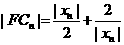 .
.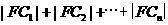
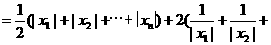 …
…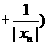
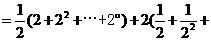 …
…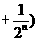
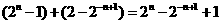 .
.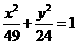 有公共焦点,且离心率
有公共焦点,且离心率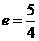 的双曲线的方程.
的双曲线的方程.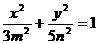 和双曲线
和双曲线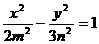 有公共的焦点,那么双曲线的渐近线方程是
有公共的焦点,那么双曲线的渐近线方程是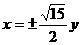 B.
B.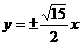 C.
C.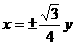 D.
D.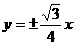
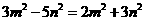 ,即
,即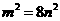 ,即双曲线方程为
,即双曲线方程为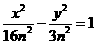 ,故双曲线的渐近线方程是
,故双曲线的渐近线方程是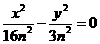 ,即
,即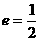 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线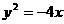 的焦点重合, 则此椭圆方程为( )
的焦点重合, 则此椭圆方程为( )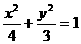 B.
B.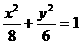
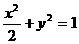 D.
D.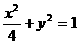
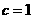 ,又
,又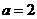 ,进而
,进而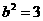 ,所以椭圆方程为
,所以椭圆方程为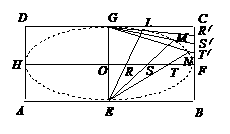 如图,矩形ABCD中,
如图,矩形ABCD中,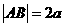 ,
,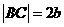 ,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,
,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,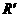 ,
,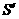 ,
,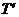 是线段CF的四等分点.请证明直线ER与
是线段CF的四等分点.请证明直线ER与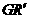 、ES与
、ES与 、ET与
、ET与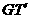 的交点L,M,N在同一个椭圆上.
的交点L,M,N在同一个椭圆上.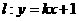 与双曲线
与双曲线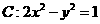 的右支交于不同的两点A、B.若双曲线C的右焦点F在以AB为直径的圆上时,则实数
的右支交于不同的两点A、B.若双曲线C的右焦点F在以AB为直径的圆上时,则实数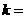 .
.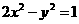 整理,得
整理,得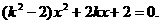 ……①
……①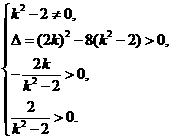 解得
解得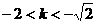 .
.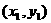 、
、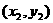 ,则由①式得
,则由①式得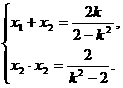 ……②
……②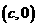 在以AB为直径的圆上,则由FA⊥FB得:
在以AB为直径的圆上,则由FA⊥FB得: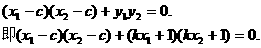
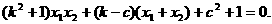 ……③
……③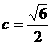 代入③式化简,得
代入③式化简,得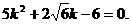
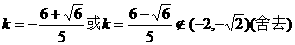 ,故
,故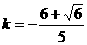 .
.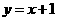 .(求解过程略)
.(求解过程略)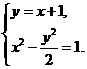 得
得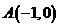 、
、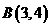 .
.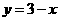 .
.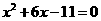 .
.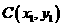 ,
,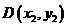 以及CD的中点为
以及CD的中点为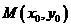 ,
,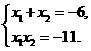 从而
从而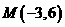 .
.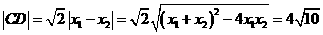 .
.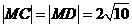 .
.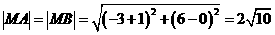 .
.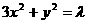 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.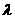 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;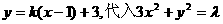 整理,得
整理,得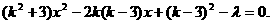 ①
①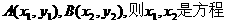 ①的两个不同的根,
①的两个不同的根,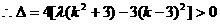 ②
②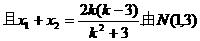 是线段AB的中点,得
是线段AB的中点,得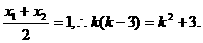
 ).
).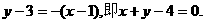
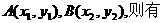
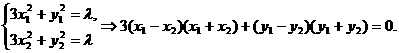
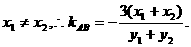
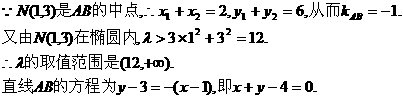
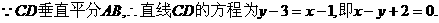 代入椭圆方程,整理得
代入椭圆方程,整理得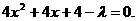 ③
③ ③的两根,
③的两根,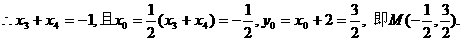
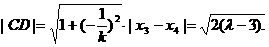 ④
④
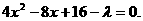 ⑤
⑤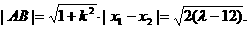 ⑥
⑥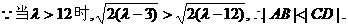
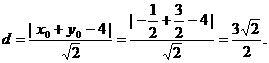 ⑦
⑦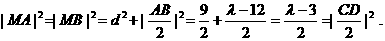
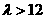 时,A、B、C、D四点均在以M为圆心,
时,A、B、C、D四点均在以M为圆心,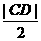 为半径的圆上.
为半径的圆上. △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角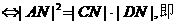
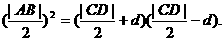 ⑧
⑧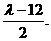
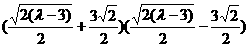
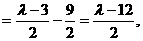
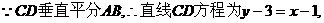 代入椭圆方程,整理得
代入椭圆方程,整理得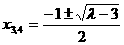 .
.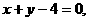 代入椭圆方程,整理得
代入椭圆方程,整理得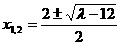 .
.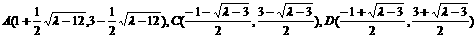
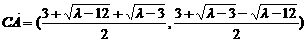
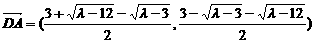
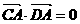 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.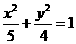 上的一点,且以点P及焦点
上的一点,且以点P及焦点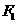 ,
,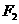 为顶点的三角形的面积等于1,求点P的坐标.
为顶点的三角形的面积等于1,求点P的坐标.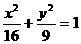 的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为
的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 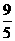 B.3 C.
B.3 C.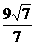 D.
D.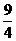
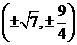 ,则点P到x轴的距离为
,则点P到x轴的距离为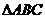 的顶点B、C在椭圆
的顶点B、C在椭圆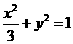 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则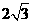 B.6 C.
B.6 C.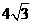 D.12
D.12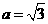 ,而根据椭圆的定义可知
,而根据椭圆的定义可知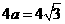 ,故选C.
,故选C.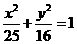 的右焦点
的右焦点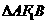 的周长;
的周长;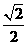 B.
B.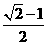 C.
C.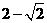 D.
D.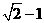
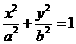 ,依题意,显然有
,依题意,显然有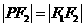 ,则
,则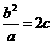 ,即
,即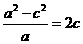 ,即
,即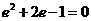 ,解得
,解得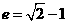 .选D.
.选D.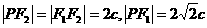 .
.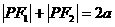 ,∴
,∴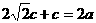 ,∴
,∴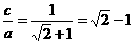 .故选D.
.故选D.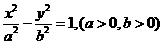 的左,右焦点分别为
的左,右焦点分别为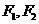 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且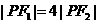 ,则此双曲线的离心率e的最大值为
.
,则此双曲线的离心率e的最大值为
.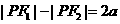 ,又已知
,又已知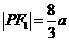 ,
,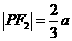 ,在
,在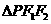 中,由余弦定理,得
中,由余弦定理,得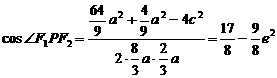 ,要求
,要求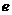 的最大值,即求
的最大值,即求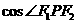 的最小值,当
的最小值,当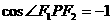 时,解得
时,解得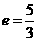 .即
.即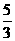 .
.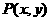 ,由焦半径公式得
,由焦半径公式得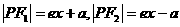 ,∵
,∵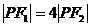 ,∴
,∴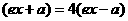 ,∴
,∴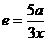 ,∵
,∵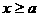 ,∴
,∴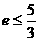 ,∴
,∴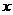 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,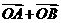 与
与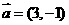 共线.
共线.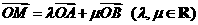 ,证明
,证明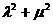 为定值.
为定值.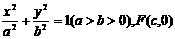 ,
,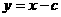 ,代入
,代入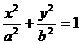 ,化简得
,化简得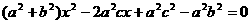 .
.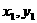 ),B
),B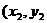 ),则
),则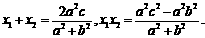
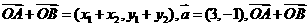 与
与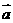 共线,得
共线,得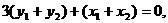 又
又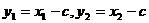 ,
,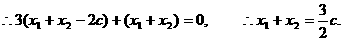
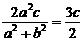 ,所以
,所以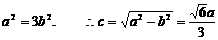 ,
,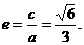
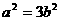 ,所以椭圆
,所以椭圆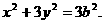
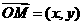 ,由已知得
,由已知得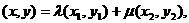
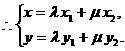
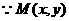 在椭圆上,
在椭圆上,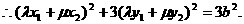
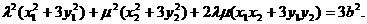 ①
①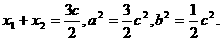
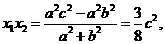
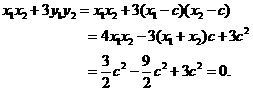
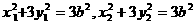 ,代入①得
,代入①得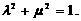
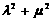 为定值,定值为1.
为定值,定值为1.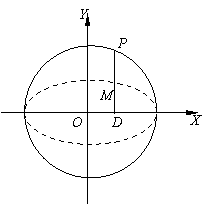 (人教A版选修1-1,2-1第39页例2)
(人教A版选修1-1,2-1第39页例2)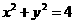 上任取一点P,过点P作X轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?
上任取一点P,过点P作X轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?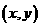 ,点P的坐标为
,点P的坐标为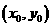 ,则
,则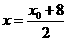 ,
,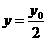 .即
.即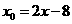 ,
,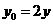 .
.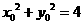 .
.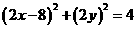 ,
,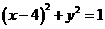 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.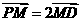 .当点P在圆上运动时,求点M的轨迹方程.
.当点P在圆上运动时,求点M的轨迹方程.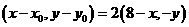 ,
,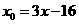 ,
,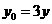 .
.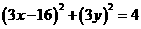 ,
,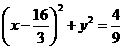 ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程.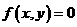 上的任一点,定点D的坐标为
上的任一点,定点D的坐标为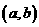 ,若点M满足
,若点M满足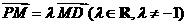 .当点P在曲线
.当点P在曲线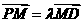 ,得
,得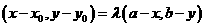 ,
,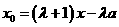 ,
,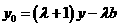 .
.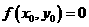 .
. ,这就是动点M的轨迹方程.
,这就是动点M的轨迹方程. ,则
,则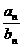 =______
=______