摘要：※如图在二面角中和分别为 平面a和b的法向量若二面角,记二面角的大小为q. (ⅰ)若该二面角为锐二面角.则或(依据两平面法向量的方向而定).但总有=.所以此时. (ⅱ)若二面角为钝二面角. 则或 (依据两平面法向量的方向而定). 但总有= 所以此时 [例3]已知三棱锥P-ABCD中PA⊥面ABCD.底面ABCD为菱形. ∠BAD=600.AB=2.PA=4.E为PC的中点. (1)求证:平面BDE⊥平面ABCD (2)求B-DE-C的大小 证明: (2)设AC∩BD=O.连结OE. 以O为原点建立空间直角坐标系 由(1)得为平面EBD的法量.. 设平面CDE的法向量 , 所以B-DE-C为.
网址：http://m.1010jiajiao.com/timu3_id_520246[举报]
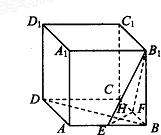
如图，在棱长为a的正方体ABCD-A1B1C1D1中，E、F分别为棱A1B1和B1C1的中点．（1）求二面角B1-BF-E的大小．
（2）求点D到平面BEF的距离．
（3）能否在棱B1B上找到一点M，使DM⊥面BEF？若能，请确定点M的位置；若不能，请说明理由． 查看习题详情和答案>>
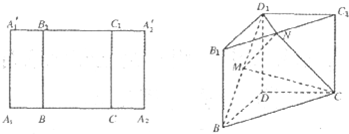
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，M、N分别为B1B和A1D的中点．（Ⅰ）求直线MN与平面ADD1A1所成角的大小；
（Ⅱ）求二面角A-MN-A1的余弦值．
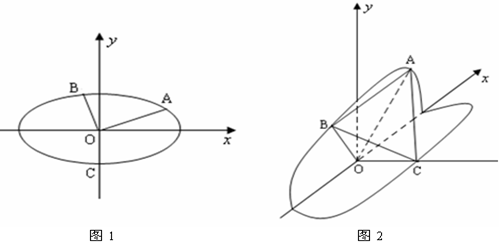
如图1，椭圆
+
=1的下顶点为C，A，B分别在椭圆的第一象限和第二象限的弧上运动，满足
⊥
，其中O为坐标原点，现沿x轴将坐标平面折成直二面角．如图2所示，在空间中，解答下列问题：
（1）证明：OC⊥AB；
（2）设二面角O-BC-A的平面角为α，二面角O-AC-B的平面角为β，二面角O-AB-C的平面角为θ，求证：cos2α+cos2β+cos2θ=1；
（3）求三棱锥O-ABC的体积的最小值．
查看习题详情和答案>>
| x2 |
| 9 |
| y2 |
| 4 |
| OA |
| OB |
（1）证明：OC⊥AB；
（2）设二面角O-BC-A的平面角为α，二面角O-AC-B的平面角为β，二面角O-AB-C的平面角为θ，求证：cos2α+cos2β+cos2θ=1；
（3）求三棱锥O-ABC的体积的最小值．
如图，在棱长为a的正方体ABCD-A1B1C1D1中，E、F分别为棱AB和BC的中点，EF交BD于H．