20、(本小题满分12分)设函数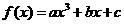
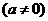 为奇函数,其图象在点
为奇函数,其图象在点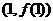 处的切线与直线
处的切线与直线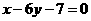 垂直,导函数
垂直,导函数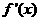 的最小值为
的最小值为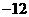 .
.
(Ⅰ)求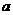 ,
,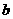 ,
,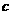 的值;
的值;
(Ⅱ)求函数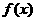 的单调递增区间,并求函数
的单调递增区间,并求函数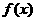 在
在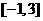 上的最大值和最小值.
上的最大值和最小值.
解析:本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.
(Ⅰ)∵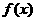 为奇函数,
为奇函数,
∴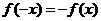
即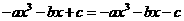
∴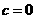
∵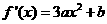 的最小值为
的最小值为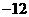
∴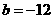
又直线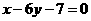 的斜率为
的斜率为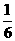
因此,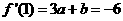
∴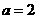 ,
,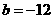 ,
,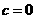 .
.
(Ⅱ)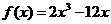 .
.
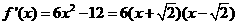 ,列表如下:
,列表如下:
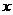 |
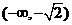 |
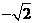 |
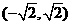 |
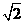 |
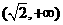 |
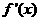 |
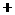 |
 |
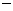 |
 |
 |
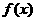 |
 |
极大 |
 |
极小 |
 |
所以函数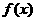 的单调增区间是
的单调增区间是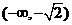 和
和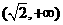
∵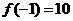 ,
,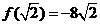 ,
,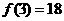
∴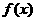 在
在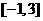 上的最大值是
上的最大值是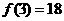 ,最小值是
,最小值是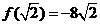 .
.
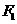 、
、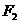 分别是椭圆
分别是椭圆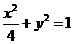 的左、右焦点.
的左、右焦点.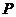 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且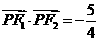 ,求点
,求点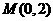 的直线
的直线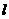 与椭圆交于同的两点
与椭圆交于同的两点 、
、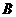 ,且
,且 为锐角(其中
为锐角(其中 为作标原点),求直线
为作标原点),求直线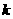 的取值范围.
的取值范围.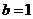 ,
,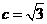 .
.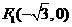 ,
,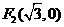 .设
.设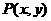
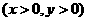 .则
.则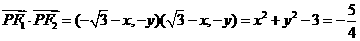 ,又
,又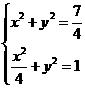 ,解得
,解得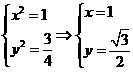 ,
,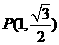 .
.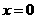 不满足题设条件.可设
不满足题设条件.可设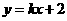 ,设
,设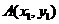 ,
,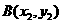 .
.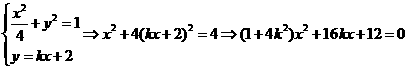
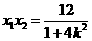 ,
,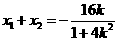
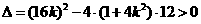
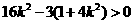 ,
,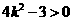 ,得
,得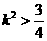 .①
.①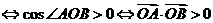 ,
,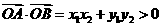
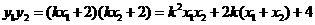
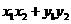
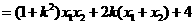
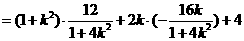
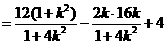
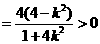
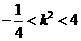 .②
.②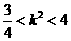 ,∴
,∴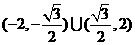 .
.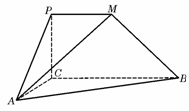 (本小题满分12分)如图,平面
(本小题满分12分)如图,平面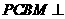 平面
平面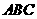 ,
,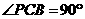 ,
,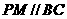 ,直线
,直线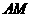 与直线
与直线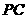 所成的角为60°,又
所成的角为60°,又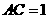 ,
,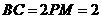 ,
,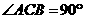 .
.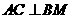 ;
;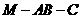 的大小;
的大小;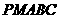 的体积.
的体积.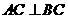 ,
,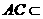 平面
平面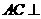 平面
平面
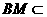 平面
平面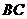 的中点
的中点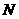 ,则
,则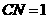 .连接
.连接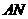 、
、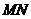 .
.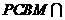 平面
平面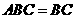 ,
,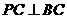 .
.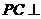 平面
平面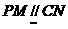 ,∴
,∴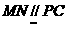 ,从而
,从而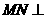 平面
平面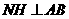 于
于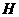 ,连结
,连结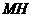 ,则由三垂线定理知
,则由三垂线定理知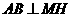 .
.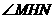 为二面角
为二面角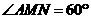 .
. 中,由勾股定理得
中,由勾股定理得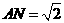 .
. 中,
中,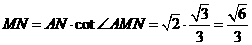 .
.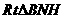 中,
中,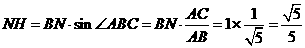 .
.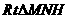 中,
中,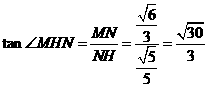
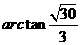
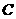 为原点建立空间直角坐标系
为原点建立空间直角坐标系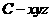 .
.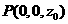
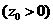 ,
,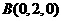 ,
,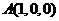 ,
,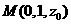 .
.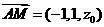 ,
,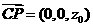
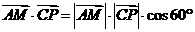
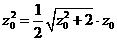 ,解得
,解得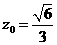 .
.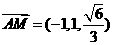 ,
,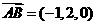
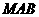 的一个法向量为
的一个法向量为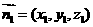 ,则
,则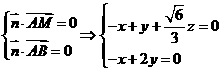 ,取
,取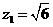 ,得
,得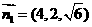
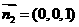
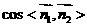
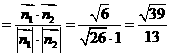
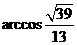 .
.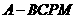
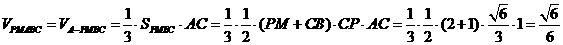 .
.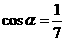 ,
,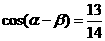 ,且
,且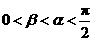 .
.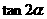 的值;
的值;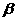 .
.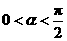 ,得
,得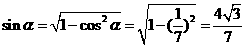 .
.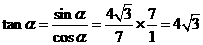 .
.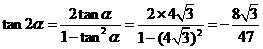 .
.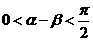 .
.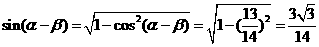 .
.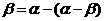 ,得
,得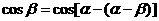
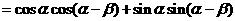
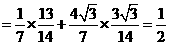
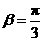 .
.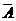 来算,有
来算,有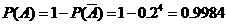
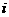 件”
件” 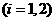 为事件
为事件 .
.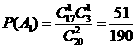
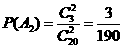
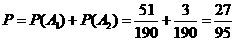 .
.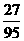 .
.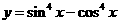 的最小正周期是
的最小正周期是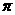 ;
;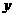 轴上的角的集合是
轴上的角的集合是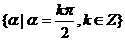 ;
;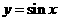 的图象和函数
的图象和函数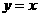 的图象有3个公共点;
的图象有3个公共点;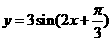 的图象向右平移
的图象向右平移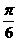 得到
得到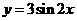 的图象;
的图象;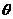 为第一象限角的充要条件是
为第一象限角的充要条件是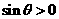
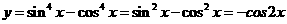 ,正确;②错误;③
,正确;②错误;③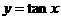 和
和 的方程是
的方程是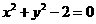 ,
, 的方程是
的方程是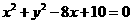 ,由动点
,由动点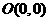 ,半径
,半径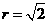 ;
;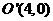 ,半径
,半径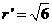 .设
.设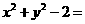
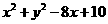 ,
,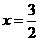 .
.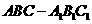 中,侧棱长为
中,侧棱长为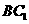 与侧面
与侧面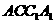 所成的角是____________
所成的角是____________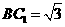 ,点
,点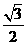 ,∴
,∴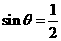 ,
,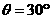 .
. 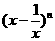 的展开式中的第5项为常数项,那么正整数
的展开式中的第5项为常数项,那么正整数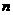 的值是
.
的值是
.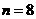 .
.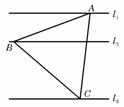 如图,
如图, 、
、 、
、 是同一平面内的三条平行直线,
是同一平面内的三条平行直线,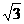 (B)
(B)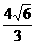
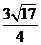 (D)
(D)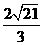
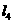 ,以
,以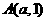 、
、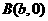 、
、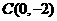 ,由
,由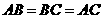 知
知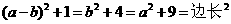 ,检验A:
,检验A: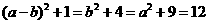 ,无解;检验B:
,无解;检验B: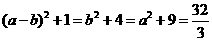 ,无解;检验D:
,无解;检验D: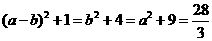 ,正确.本题是把关题.在基础中考能力,在综合中考能力,在应用中考能力,在新型题中考能力全占全了.是一道精彩的好题.可惜区分度太小.
,正确.本题是把关题.在基础中考能力,在综合中考能力,在应用中考能力,在新型题中考能力全占全了.是一道精彩的好题.可惜区分度太小.