摘要:如图.平面平面...直线与直线所成的角为60°.又... (Ⅰ)求证:, (Ⅱ)求二面角的大小, (Ⅲ)求多面体的体积. 解析:本题主要考查异面直线所成的角.平面与平面垂直.二面角.棱锥体积等有关知识.考查思维能力和空间想象能力.应用向量知识解决数学问题的能力.化归转化能力和推理运算能力. (Ⅰ)∵平面平面..平面. ∴平面 又∵平面 ∴ (Ⅱ)取的中点.则.连接.. ∵平面平面.平面平面.. ∴平面. ∵.∴.从而平面. 作于.连结.则由三垂线定理知. 从而为二面角的平面角. ∵直线与直线所成的角为60°. ∴ . 在中.由勾股定理得. 在中.. 在中.. 在中. 故二面角的大小为 (Ⅱ)如图以为原点建立空间直角坐标系. 设. 有... . 由直线与直线所成的角为60°.得 即.解得. ∴. 设平面的一个法向量为.则 由.取.得 取平面的一个法向量为 则 由图知二面角为锐二面角.故二面角的大小为. (Ⅲ)多面体就是四棱锥 .
网址:http://m.1010jiajiao.com/timu3_id_515328[举报]
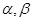 ,
,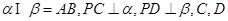 是垂足.
是垂足.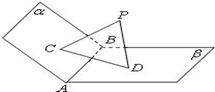
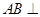 平面
平面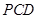 ;
;
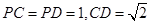 ,求证:
,求证: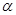
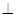
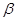 .
. 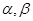 ,
,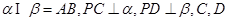 是垂足.
是垂足.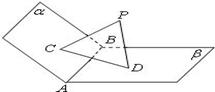
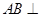 平面
平面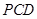 ;
; 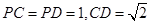 ,求证:
,求证: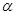
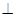
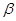 .
. ,
, 是垂足.
是垂足.
 平面
平面 ;
;  ,求证:
,求证:

 .
. (本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;
(本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;