摘要:抽象函数.抽象函数问题是近几年高考中函数类问题的一个新的热点.由于具体函数与抽象函数之间是特殊化与一般化的关系.因而抽象函数问题的解决方法更加灵活多样.既可以采用特殊化方法.又可以回归函数的各种性质.有利于考查学生的抽象思维能力.故而应引起我们的高度重视. 例11.已知的解析式可取为 (A) (B) (C) (D) 例12. 若和g(x)都是定义在实数集R上的函数.且方程有实数解.则不可能是 (A) (B) (C) (D) 例13.给出四个函数.分别满足: ① ② ③ ④ 又给出四个函数的图像.则正确的匹配方案是 (A)①-a ②-b ③-c ④-d (B)①-b ②-c ③-a ④-d (C)①-c ②-a ③-b ④-d (D)①-d ②-a ③-b ④-c 例14.已知的定义域为,若与互为反函数且 (为非零常数),则= 例15. 函数的定义域为.对于任意实数..有: 且 (1)求证: (2)若..证明:在递减
网址:http://m.1010jiajiao.com/timu3_id_510116[举报]
(2003•朝阳区一模)抽象函数是由特殊的、具体的函数抽象而得到的.如正比例函数f(x)=kx(k≠0),f(x1)=kx1,f(x2)=kx2,f(x1+x2)=k(x1+x2)=kx1+kx2=f(x1)+f(x2)可抽象为f(x+y)=f(x)+f(y).写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可).
查看习题详情和答案>>
| 特殊函数 | 抽象函数 | ||
f(x)=xα f(x)=xα |
f(xy)=f(x)f(y) | ||
f(x)=ax(a>0且a≠1) f(x)=ax(a>0且a≠1) |
f(x+y)=f(x)f(y) | ||
f(x)=logax(a>0且a≠1) f(x)=logax(a>0且a≠1) |
f(xy)=f(x)+f(y) | ||
f(x)=tanx f(x)=tanx |
f(x+y)=
|
抽象函数是由特殊的、具体的函数抽象而得到的.如正比例函数f(x)=kx(k≠0),f(x1)=kx1,f(x2)=kx2,f(x1+x2)=k(x1+x2)=kx1+kx2=f(x1)+f(x2)可抽象为f(x+y)=f(x)+f(y).写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可).
| 特殊函数 | 抽象函数 |
| ________ | f(xy)=f(x)f(y) |
| ________ | f(x+y)=f(x)f(y) |
| ________ | f(xy)=f(x)+f(y) |
| ________ | f(x+y)=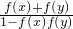 |
抽象函数是由特殊的、具体的函数抽象而得到的.如正比例函数f(x)=kx(k≠0),由f(x1)=kx1,f(x2)=kx2抽象得到f(x1+x2)=f(x1)+f(x2)可抽象为f(x+y)=f(x)+f(y).写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可).
 查看习题详情和答案>>
查看习题详情和答案>>