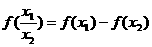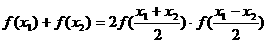(1)一元一次函数: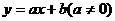 ,当
,当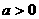 时,是增函数;当
时,是增函数;当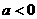 时,是减函数;
时,是减函数;
(2)一元二次函数:
一般式: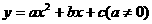 ;对称轴方程是
;顶点为
;
;对称轴方程是
;顶点为
;
两点式: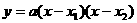 ;对称轴方程是 ;与
;对称轴方程是 ;与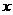 轴的交点为
;
轴的交点为
;
顶点式: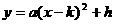 ;对称轴方程是
;顶点为
;
;对称轴方程是
;顶点为
;
①一元二次函数的单调性:
当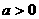 时: 为增函数; 为减函数;当
时: 为增函数; 为减函数;当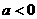 时: 为增函数; 为减函数;
时: 为增函数; 为减函数;
②二次函数求最值问题:首先要采用配方法,化为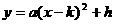 的形式,
的形式,
Ⅰ、若顶点的横坐标在给定的区间上,则
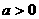 时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;
时:在顶点处取得最小值,最大值在距离对称轴较远的端点处取得;
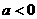 时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;
时:在顶点处取得最大值,最小值在距离对称轴较远的端点处取得;
Ⅱ、若顶点的横坐标不在给定的区间上,则
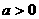 时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;
时:最小值在距离对称轴较近的端点处取得,最大值在距离对称轴较远的端点处取得;
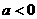 时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得;
时:最大值在距离对称轴较近的端点处取得,最小值在距离对称轴较远的端点处取得;
有三个类型题型:
(1)顶点固定,区间也固定。如: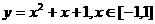
(2)顶点含参数(即顶点变动),区间固定,这时要讨论顶点横坐标何时在区间之内,何时在区间之外。
(3)顶点固定,区间变动,这时要讨论区间中的参数.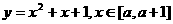
③二次方程实数根的分布问题: 设实系数一元二次方程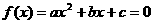 的两根为
的两根为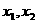 ;则:
;则:
|
根的情况 |
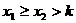 |
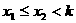 |
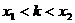 |
|
等价命题 |
在区间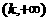 上有两根 上有两根 |
在区间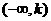 上有两根 上有两根 |
在区间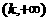 或 或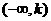 上有一根 上有一根 |
|
充要条件 |
|
|
|
注意:若在闭区间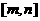 讨论方程
讨论方程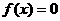 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间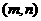 上实根分布的情况,得出结果,在令
上实根分布的情况,得出结果,在令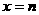 和
和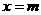 检查端点的情况。
检查端点的情况。
(3)反比例函数: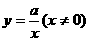
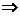
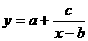
(4)指数函数: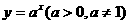
指数运算法则: ; ; 。
指数函数:y=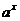 (a>o,a≠1),图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(a>o,a≠1),图象恒过点(0,1),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(5)对数函数: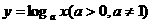
指数运算法则: ; ; ;
对数函数:y=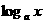 (a>o,a≠1) 图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
(a>o,a≠1) 图象恒过点(1,0),单调性与a的值有关,在解题中,往往要对a分a>1和0<a<1两种情况进行讨论,要能够画出函数图象的简图。
注意:(1)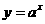 与
与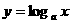 的图象关系是
;
的图象关系是
;
(2)比较两个指数或对数的大小的基本方法是构造相应的指数或对数函数,若底数不相同时转化为同底数的指数或对数,还要注意与1比较或与0比较。
(3)已知函数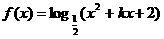 的定义域为
的定义域为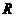 ,求
,求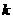 的取值范围。
的取值范围。
已知函数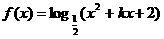 的值域为
的值域为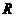 ,求
,求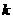 的取值范围。
的取值范围。
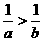 。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。
。即不等式两边同号时,不等式两边取倒数,不等号方向要改变。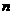 次多项式的导数问题属于较难类型。
次多项式的导数问题属于较难类型。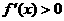 与
与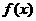 为增函数的关系。
为增函数的关系。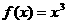 在
在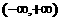 上单调递增,但
上单调递增,但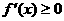 ,∴
,∴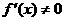 时,
时,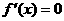 的根作为分界点,因为规定
的根作为分界点,因为规定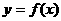 (1)分析
(1)分析 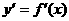 (3)解不等式
(3)解不等式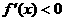 ,解集在定义域内的部分为减区间。
,解集在定义域内的部分为减区间。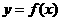 在某个区间内可导。
在某个区间内可导。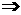 f/(x0)=0
f/(x0)=0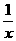 )/=-x-2 (f(x)±g(x))/=
f/(x)±g/(x) (k•f(x))/=
k•f/(x)
)/=-x-2 (f(x)±g(x))/=
f/(x)±g/(x) (k•f(x))/=
k•f/(x) 
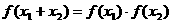 ;
;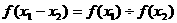
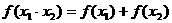 ;
;