摘要：1．求导法则: (c)/=0 这里c是常数.即常数的导数值为0. (xn)/=nxn-1 特别地:(x)/=1 (x-1)/= ()/=-x-2 /= f/(x)±g//= k•f/(x)
网址：http://m.1010jiajiao.com/timu3_id_507744[举报]
试根据复合函数的求导法则，研究函数f（x）=xx（x＞0）的性质，并回答：下列命题中假命题的个数是（ ）
①f（x）的极大值为1；
②f（x）的极小值为1；
③f（x）的一个单调递增区间是(
，10)．
①f（x）的极大值为1；
②f（x）的极小值为1；
③f（x）的一个单调递增区间是(
| 1 |
| 10 |
| A、0 | B、1 | C、2 | D、3 |
请先阅读：
在等式cos2x=2cos2x-1（x∈R）的两边求导，得：（cos2x）′=（2cos2x-1）′，由求导法则，得（-sin2x）•2=4cosx•（-sinx），化简得等式：sin2x=2cosx•sinx．
（1）利用上题的想法（或其他方法），结合等式（1+x）n=Cn0+Cn1x+Cn2x2+…+Cnnxn（x∈R，正整数n≥2），证明：n[(1+x)n-1-1]=
k
xk-1．
（2）对于正整数n≥3，求证：
（i）
(-1)kk
=0；
（ii）
(-1)kk2
=0；
（iii）
=
．
查看习题详情和答案>>
在等式cos2x=2cos2x-1（x∈R）的两边求导，得：（cos2x）′=（2cos2x-1）′，由求导法则，得（-sin2x）•2=4cosx•（-sinx），化简得等式：sin2x=2cosx•sinx．
（1）利用上题的想法（或其他方法），结合等式（1+x）n=Cn0+Cn1x+Cn2x2+…+Cnnxn（x∈R，正整数n≥2），证明：n[(1+x)n-1-1]=
| n |
 |
| k=2 |
| C | k n |
（2）对于正整数n≥3，求证：
（i）
| n |
|
| k=1 |
| C | k n |
（ii）
| n |
|
| k=1 |
| C | k n |
（iii）
| n |
|
| k=1 |
| 1 |
| k+1 |
| C | k n |
| 2n+1-1 |
| n+1 |
请先阅读：
设可导函数 f（x） 满足f（-x）=-f（x）（x∈R）．
在等式f（-x）=-f（x） 的两边对x求导，
得（f（-x））′=（-f（x））′，
由求导法则，得f′（-x）•（-1）=-f′（x），
化简得等式f′（-x）=f′（x）．
（Ⅰ）利用上述想法（或其他方法），结合等式(1+x)n=
+
x+
x2+…+
xn（x∈R，整数n≥2），证明：n[(1+x)n-1-1]=2
x+3
x2+4
x3+…+n
xn-1；
（Ⅱ）当整数n≥3时，求
-2
+3
-…+(-1)n-1n
的值；
（Ⅲ）当整数n≥3时，证明：2
-3•2
+4•3
+…+(-1)n-2n(n-1)
=0．
查看习题详情和答案>>
设可导函数 f（x） 满足f（-x）=-f（x）（x∈R）．
在等式f（-x）=-f（x） 的两边对x求导，
得（f（-x））′=（-f（x））′，
由求导法则，得f′（-x）•（-1）=-f′（x），
化简得等式f′（-x）=f′（x）．
（Ⅰ）利用上述想法（或其他方法），结合等式(1+x)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
（Ⅱ）当整数n≥3时，求
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
（Ⅲ）当整数n≥3时，证明：2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
（
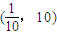）的两边求导，得：
，由求导法则，得
，化简得等式：
．
（
），证明：
＝
．
，求证：（i）
＝0；
＝0；
．
．