摘要:2 求曲线的方程.考查坐标法的思想和方法.从不同思维层次上反映数学能力. 例2 双曲线为渐近线且过点. (1) 求双曲线的方程, (2) 已知动点与曲线的两个焦点所连线段长的和为定长.且这两条线段夹角的余弦最小值为.求动点的轨迹方程, (3) 在轴正半轴上是否存在一点.使得与的轨迹方程上的点的最短距离为1?若存在.求出点坐标,若不存在.说明理由. 分析:本题主要考查双曲线.椭圆的方程.基本不等式及二次函数的最值.利用待定系数法可求出指定圆锥曲线的方程.本题把最值问题联系起来.体现了知识的整体性和系统性.既考查基础知识和基本方法.又渗透数学思想.突出对能力的考查.从不同的思维层次上反映能力. (Ⅰ)设双曲线方程为.故 (Ⅱ)由题意.点轨迹以为焦点的椭圆.设方程为:.则 ① 记.则. 由知当即P为椭圆短轴端点时.有最小值.并且②.由①.②可得.故动点P的轨迹方程为:. (Ⅲ)设是以上轨迹上任一点.则..又. 对称轴. (1)若即.则当时..不合. (2)若.即.则当时.或. 故存在点或满足条件.
网址:http://m.1010jiajiao.com/timu3_id_501888[举报]
抛物线C1的方程是(y-2)2=-8(x+2),曲线C2与C1关于点(-1,1)对称.
(Ⅰ)求曲线的方程;
(Ⅱ)过点(8,0)的直线l交曲线C2于M、N两点,问在坐标平面上能否找到某个定点Q,不论直线l如何变化,总有∠MQN=90°.若找不到,请说明理由;若能找到,写出满足要求的所有的点Q的坐标.
查看习题详情和答案>>
(Ⅰ)求曲线的方程;
(Ⅱ)过点(8,0)的直线l交曲线C2于M、N两点,问在坐标平面上能否找到某个定点Q,不论直线l如何变化,总有∠MQN=90°.若找不到,请说明理由;若能找到,写出满足要求的所有的点Q的坐标.
(2013•汕尾二模)已知F1(-
,0),F2(
,0)为平面内的两个定点,动点P满足|PF1|+|PF2|=4,记点P的轨迹为曲线Γ.
(Ⅰ)求曲线Γ的方程;
(Ⅱ)判断原点O关于直线x+y-1=0的对称点R是否在曲线Γ包围的范围内?说明理由.
(注:点在曲线Γ包围的范围内是指点在曲线Γ上或点在曲线Γ包围的封闭图形的内部)
(Ⅲ)设点O为坐标原点,点A,B,C是曲线Γ上的不同三点,且
+
+
=
.试探究:直线AB与OC的斜率之积是否为定值?证明你的结论.
查看习题详情和答案>>
| 2 |
| 2 |
(Ⅰ)求曲线Γ的方程;
(Ⅱ)判断原点O关于直线x+y-1=0的对称点R是否在曲线Γ包围的范围内?说明理由.
(注:点在曲线Γ包围的范围内是指点在曲线Γ上或点在曲线Γ包围的封闭图形的内部)
(Ⅲ)设点O为坐标原点,点A,B,C是曲线Γ上的不同三点,且
| OA |
| OB |
| OC |
| 0 |
 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(-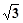 ,0)和F2(
,0)和F2( 与曲线
与曲线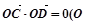 为坐标原点),求直线
为坐标原点),求直线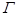 上任意一点
上任意一点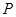 到两个定点
到两个定点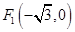 和
和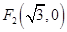 的距离之和为4.
的距离之和为4.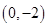 的直线
的直线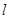 与曲线
与曲线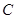 、
、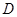 两点,且
两点,且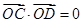 (
(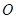 为坐标原点),求直线
为坐标原点),求直线