摘要: 分值.题型.难度设置 圆锥曲线是高中数学的重要内容之一.分值约占14﹪.即20分左右.题型一般为二小一大.例如.2005年高考为一道选择题.一道填空题 一道解答题.小题基础灵活.解答题一般在中等以上.一般具有较高的区分度. 考试内容:椭圆.双曲线.抛物线的定义.标准方程.简单的几何性质.椭圆的参数方程. 主要题型:(1)定义及简单几何性质的灵活运用,(2)求曲线方程(含指定圆锥曲线方程及轨迹方程),(3)直线与圆锥曲线的位置关系问题(交点.弦长.中点弦及斜率.对称问题).确定参数的取值范围,(4)在导数.不等式.函数.向量等知识网络交汇点上的问题.
网址:http://m.1010jiajiao.com/timu3_id_501885[举报]
试题大类:高考真题;题型:解答题;学期:2008年;单元:2008年普通高等学校夏季招生考试数学文史类(重庆卷);知识点:空间直线和平面;难度:较难;其它备注:20主观题;分值:12$如图,α和β为平面,α∩β=l,A∈α,B∈β,AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角α-l-β的大小为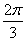 ,求:
,求:

(1)点B到平面α的距离;
(2)异面直线l与AB所成的角(用反三角函数表示).
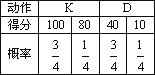
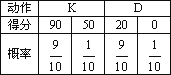
查看习题详情和答案>>2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
乙系列:
现该运动员最后一个出场,其之前运动员的最高得分为118分.
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX.