0 50188 50196 50202 50206 50212 50214 50218 50224 50226 50232 50238 50242 50244 50248 50254 50256 50262 50266 50268 50272 50274 50278 50280 50282 50283 50284 50286 50287 50288 50290 50292 50296 50298 50302 50304 50308 50314 50316 50322 50326 50328 50332 50338 50344 50346 50352 50356 50358 50364 50368 50374 50382 447348
 p是
p是  B.x
B.x  A或x
A或x 
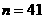 合乎条件.用反证法.假定存在X的15个子集,它们中任何7个的并不少于41个元素,而任何3个的交都为空集.因每个元素至多属于2个子集,不妨设每个元素恰好属于2个子集(否则在一些子集中添加一些元素,上述条件仍然成立),由抽屉原理,必有一个子集,设为A,至少含有
合乎条件.用反证法.假定存在X的15个子集,它们中任何7个的并不少于41个元素,而任何3个的交都为空集.因每个元素至多属于2个子集,不妨设每个元素恰好属于2个子集(否则在一些子集中添加一些元素,上述条件仍然成立),由抽屉原理,必有一个子集,设为A,至少含有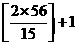 =8个元素,又设其它14个子集为
=8个元素,又设其它14个子集为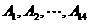 .考察不含A的任何7个子集,都对应X中的41个元素,所有不含A的7-子集组一共至少对应
.考察不含A的任何7个子集,都对应X中的41个元素,所有不含A的7-子集组一共至少对应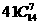 个元素.另一方面,对于元素a,若
个元素.另一方面,对于元素a,若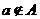 ,则
,则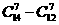 次;若
次;若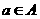 ,则
,则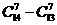 次,于是
次,于是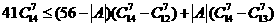
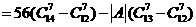
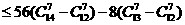 ,
,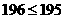 ,矛盾.
,矛盾.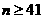 .
.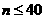 ,设
,设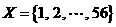 ,令
,令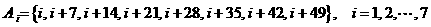 ,
,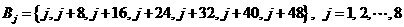 .
.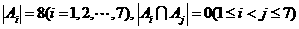 ,
,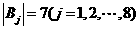 ,
,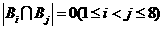 ,
,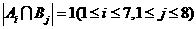 ,于是,对其中任何3个子集,必有2个同时为
,于是,对其中任何3个子集,必有2个同时为 ,或者同时为
,或者同时为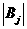 ,其交为空集.
,其交为空集.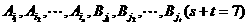 ,有
,有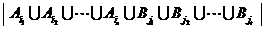
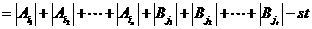
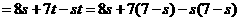
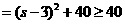 ,
,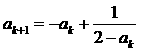 ,
,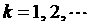 .
.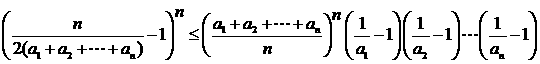 .
.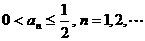 .
.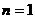 时,命题显然成立.
时,命题显然成立.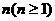 成立,即有
成立,即有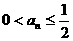 .
.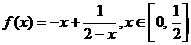 ,则
,则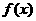 是减函数,于是
是减函数,于是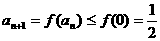 ,
,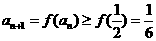
 ,
,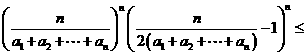
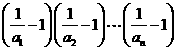 .
.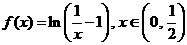 ,则
,则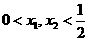 ,有
,有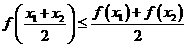 .
.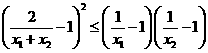 ,
,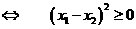 .
.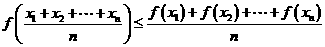 ,
,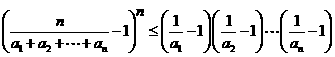 .
.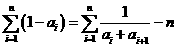
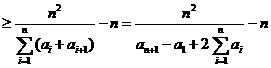
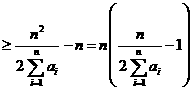 ,
,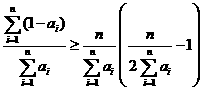 ,
,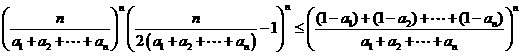
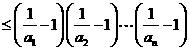 ,
,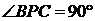 ,求证:
,求证: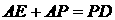 .
.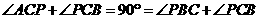 ,所以
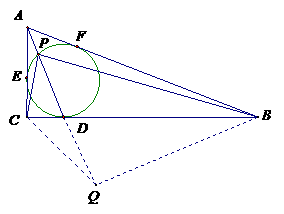
,所以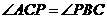 .
.
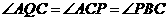 ,连接BQ,CQ,则P,B,Q,C四点共圆,令DQ=l,则由相交弦定理和切割线定理可得
,连接BQ,CQ,则P,B,Q,C四点共圆,令DQ=l,则由相交弦定理和切割线定理可得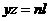 ,
①
,
①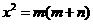 .
②
.
② ∽
∽ ,所以
,所以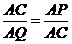 ,故
,故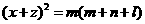 .
③
.
③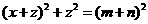 ,
④
,
④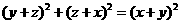 .
⑤
.
⑤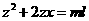 ,
⑥
,
⑥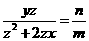 ,
,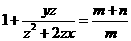 ,
⑦
,
⑦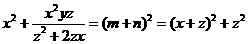 ,
,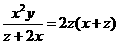 .
⑧
.
⑧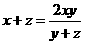 ,
⑨
,
⑨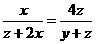 .
⑩
.
⑩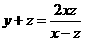 ,
11
,
11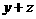 ,得
,得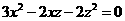 ,
,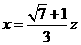 ,
,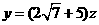 ,
,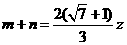 ,
,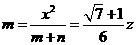 ,
,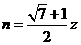 ,
,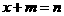 ,即
,即 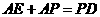 .
.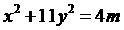
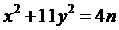
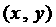 .
.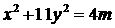 ①
①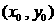 ,或有满足
,或有满足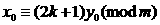 ②
②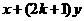
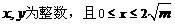
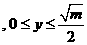 ,
,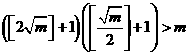 个表示,因此存在整数
个表示,因此存在整数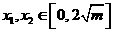 ,
,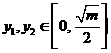 ,满足
,满足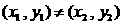 ,且
,且
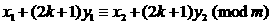 ,
,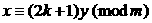 ,
③
,
③ 。由此可得
。由此可得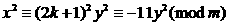 ,
,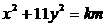 ,因为
,因为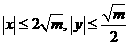 ,所以
,所以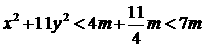 ,
,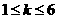 .因为m为奇数,
.因为m为奇数,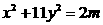 ,
,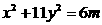 显然没有整数解.
显然没有整数解.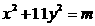 ,则
,则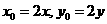 是方程①满足②的解.
是方程①满足②的解.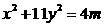 ,则
,则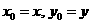 是方程①满足②的解.
是方程①满足②的解.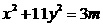 ,则
,则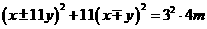 .
.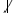 m,若
m,若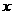
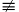
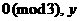
 ,且
,且 ,则
,则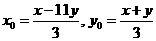 ④
④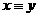
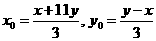 ⑤
⑤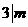 ,则公式④和⑤仍然给出方程①的整数解.若方程①有偶数解
,则公式④和⑤仍然给出方程①的整数解.若方程①有偶数解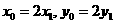 ,则
,则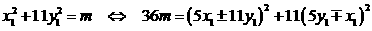 .
.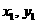 的奇偶性不同,所以
的奇偶性不同,所以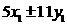 ,
,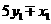 都为奇数.
都为奇数.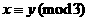 ,则
,则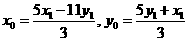 是方程①的一奇数解.
是方程①的一奇数解.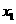
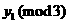 ,则
,则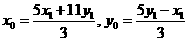 是方程①的一奇数解.
是方程①的一奇数解.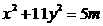 ,则
,则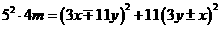 .
.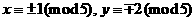 ,或
,或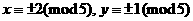 ,则
,则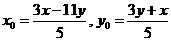 ⑥
⑥ 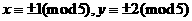 ,或
,或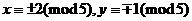 ,则
,则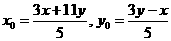 ⑦
⑦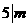 ,则公式⑥和⑦仍然给出方程①的整数解.若方程①有偶数解
,则公式⑥和⑦仍然给出方程①的整数解.若方程①有偶数解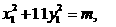
 ,
,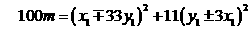 .
.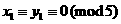 ,或者
,或者 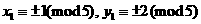 ,或者
,或者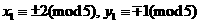 ,则
,则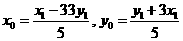 是方程①的一奇数解.
是方程①的一奇数解.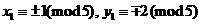 ,或
,或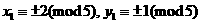 ,则
,则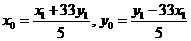
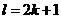 ,考虑二次方程
,考虑二次方程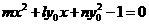 ,
⑧
,
⑧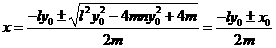 ,
,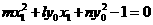 , ⑨
, ⑨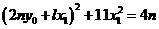 ,
,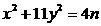 有奇数解
有奇数解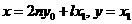 .
.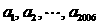 中最少有46个互不相同的数.
中最少有46个互不相同的数.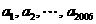 中互不相同的数大于45.
中互不相同的数大于45.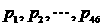 为46个互不相同的素数,构造
为46个互不相同的素数,构造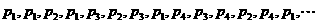 ,
,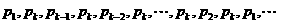 ,
,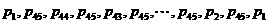 ,
,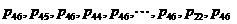 ,
,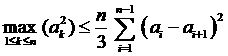 .
.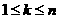 ,证明不等式成立即可.
,证明不等式成立即可.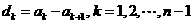 ,则
,则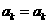 ,
,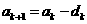 ,
,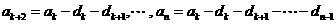 ,
,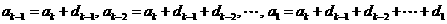 ,
,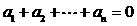 可得
可得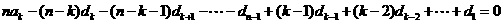 .
.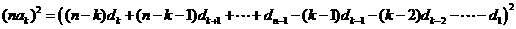
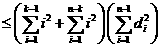
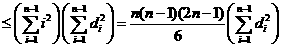
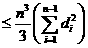 ,
, .
.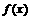 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,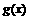 的图象与
的图象与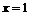 对称,且当
对称,且当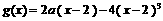 222233.
222233.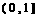 上为增函数,求
上为增函数,求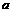 的取值范围;
的取值范围;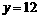 上?若存在,求出
上?若存在,求出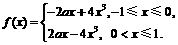 …………………………………………………4分
…………………………………………………4分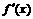 >0对x∈
>0对x∈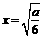 .…………10分 若
.…………10分 若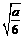 ∈
∈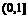 ,即0<a≤6,则
,即0<a≤6,则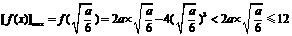 ,
,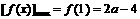 .
.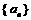 的首项为
的首项为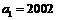 ,公比
,公比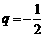 .
.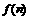 表示该数列的前n项的积,求
表示该数列的前n项的积,求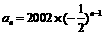 ,
,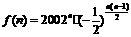 .………………………………4分
.………………………………4分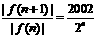 ,
,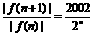 <1,∴ | f(11)
|>| f(12)
|>….………………………8分
<1,∴ | f(11)
|>| f(12)
|>….………………………8分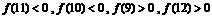 ,∴
,∴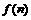 的最大值为
的最大值为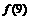 或
或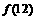 中的最大者.10分
中的最大者.10分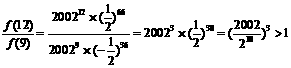 ,
,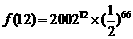 .……………………………12分
.……………………………12分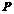 是以
是以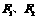 为焦点的双曲线C:
为焦点的双曲线C: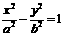 (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知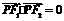 ,
,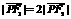 .
.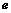 ;
;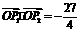 ,
,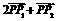 = 0,求双曲线的方程.
= 0,求双曲线的方程.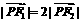 ,
,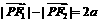 , ∴
, ∴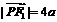 ,
,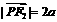 .
.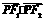 =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴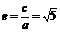 .………………………………4分
.………………………………4分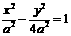 ,渐近线方程为
,渐近线方程为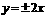 .…5分
.…5分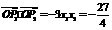 ,∴
,∴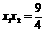 . ∵
. ∵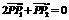 ,∴
,∴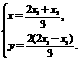 ………8分
………8分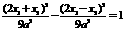 .
.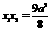 .∴
.∴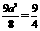 .∴
.∴ 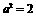 . ∴双曲线的方程为
. ∴双曲线的方程为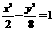 .………12分
.………12分