0 48517 48525 48531 48535 48541 48543 48547 48553 48555 48561 48567 48571 48573 48577 48583 48585 48591 48595 48597 48601 48603 48607 48609 48611 48612 48613 48615 48616 48617 48619 48621 48625 48627 48631 48633 48637 48643 48645 48651 48655 48657 48661 48667 48673 48675 48681 48685 48687 48693 48697 48703 48711 447348
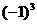 和1 B.
和1 B. 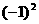 和-1 C.
和-1 C. 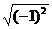 和-1 D.
和-1 D.
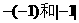


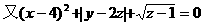
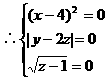
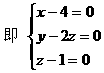
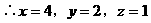
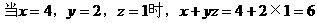
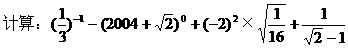
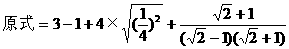
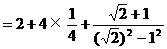
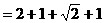
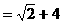
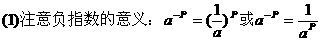
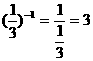
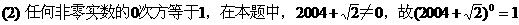

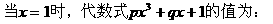
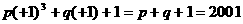
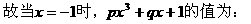
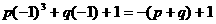
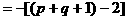
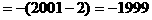
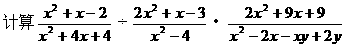
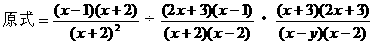
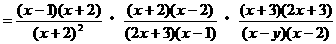
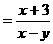

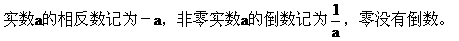
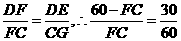 ,∴FC=40(cm).
,∴FC=40(cm).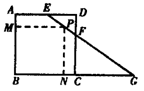
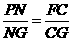 .∴NG=
.∴NG=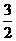 x,∴BN=120-
x,∴BN=120-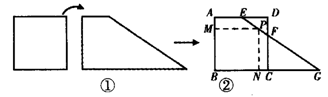
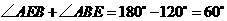 和
和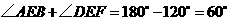 得
得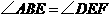 .
.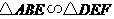

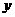 与
与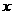 的函数表达式是
的函数表达式是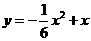
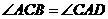 (或
(或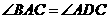 )····················································· 3分
)····················································· 3分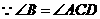 ,又
,又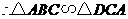 ····································································································· 5分
····································································································· 5分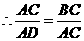 ,即
,即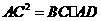 ······························· 6分
······························· 6分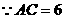 ,
,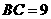 ,
,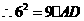 ,
,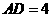 ································································ 7分
································································ 7分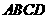 的中位线长为
的中位线长为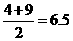 ······································································· 8分
······································································· 8分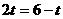 ,即
,即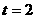 时,三角形QAP为等腰三角形;
时,三角形QAP为等腰三角形;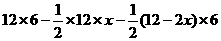 =36,即当P、Q运动时,四边形QAPC的面积不变。
=36,即当P、Q运动时,四边形QAPC的面积不变。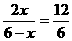 或
或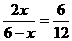 ,解之得
,解之得 或
或
 (2007长沙)如图,□
(2007长沙)如图,□ 中,
中,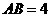 ,
,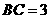 ,
,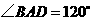 ,
,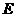 为
为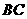 上一动点(不与
上一动点(不与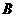 重合),作
重合),作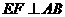 于
于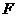 ,
, ,
,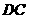 的延长线交于点
的延长线交于点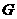 ,设
,设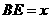 ,
,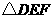 的面积为
的面积为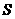 .
. ;
;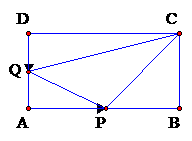 9:如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0≤ t ≤6),那么:
9:如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0≤ t ≤6),那么: