21.(2010.十堰)(本小题满分8分)暑假快到了,老家在十堰的大学生张明与王艳打算留在上海,为世博会做义工.学校争取到6个义工名额,分别安排在中国馆园区3个名额,世博轴园区2个名额,演义中心园区1个名额. 学校把分别标号为1、2、3、4、5、6的六个质地大小均相同的小球,放在不透明的袋子里,并规定标号1、2、3的到中国馆,标号4、5到世博轴,标号6的到演艺中心,让张明、王艳各摸1个.
(1)求张明到中国馆做义工的概率;
(2)求张明、王艳各自在世博轴、演艺中心做义工的概率(两人不同在一个园区内).
解:(1)如表所示,张明、王艳各摸一球可能出现的结果有6×5=30个,它们出现的可能性相等,张明到中国馆的结果有15个,∴P(张明到中国馆做义务)=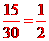 .
.
|
张明 王艳 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
(2,1) |
(3,1) |
(4,1) |
(5,1) |
(6,1) |
|
2 |
(1,2) |
|
(3,2) |
(4,2) |
(5,2) |
(6,2) |
|
3 |
(1,3) |
(2,3) |
|
(4,3) |
(5,3) |
(6,3) |
|
4 |
(1,4) |
(2,4) |
(3,4) |
|
(5,4) |
(6,4) |
|
5 |
(1,5) |
(2,5) |
(3,5) |
(4,5) |
|
(6,5) |
|
6 |
(1,6) |
(2,6) |
(3,6) |
(4,6) |
(5,6) |
|
(2)张明、王艳各自在世博轴、演艺中心的结果共4个,其概率P=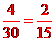 .
.
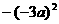 的结果是
的结果是 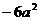 B.
B. 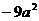 C.
C. 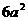 D.
D. 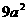
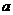 元,其支出情况如图所示,那么下列说法不正确的是
元,其支出情况如图所示,那么下列说法不正确的是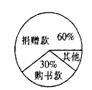
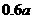 元 B.捐赠款所对应的圆心角为
元 B.捐赠款所对应的圆心角为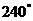
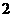 倍 D.其他支出占
倍 D.其他支出占 %
%
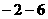 的结果是
( )中考资源网
的结果是
( )中考资源网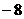 B.8 C.
B.8 C.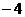 D.4
D.4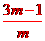 ,x1·x2=
,x1·x2=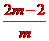
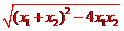 =
=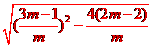 =
=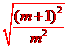 =
=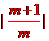 ,
,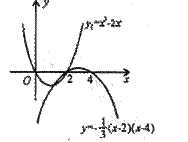 由| x1-x2|=2得
由| x1-x2|=2得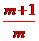 =2或
=2或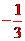
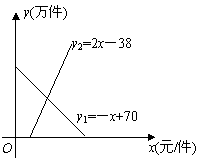
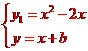 ,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;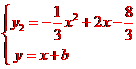 ,可得△=9-4(8+3b)=0,得b=-.
,可得△=9-4(8+3b)=0,得b=-.
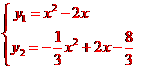
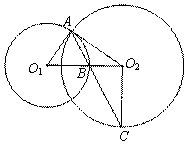

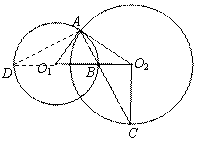 (2)延长O2O1交⊙O1于点D,连结AD.
(2)延长O2O1交⊙O1于点D,连结AD.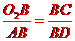
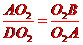

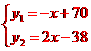 ,
,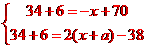 ,解得
,解得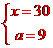
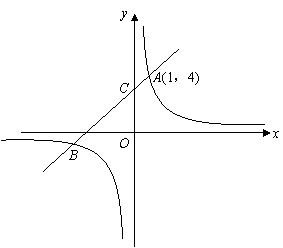

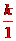 ,∴k=4,∴反比例函数的解析式为y=
,∴k=4,∴反比例函数的解析式为y=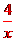 .
.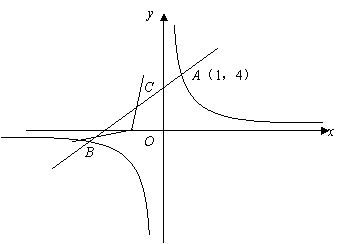 (2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4即b=4-a.
(2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4即b=4-a.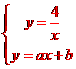 ,得ax2 +bx-4=0,即ax2 +(4-a)x-4=0,
,得ax2 +bx-4=0,即ax2 +(4-a)x-4=0,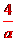 ,
,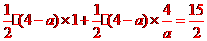 ,整理得
,整理得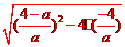 =
=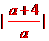 =
=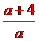 (a>0),
(a>0),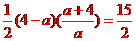 ,解得a=1或a=-16(舍去).
,解得a=1或a=-16(舍去).

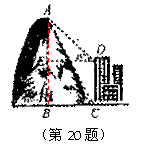

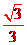 h
h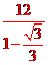 =
=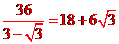 =18+6×1.73=18+10.38≈28.4(米)
=18+6×1.73=18+10.38≈28.4(米)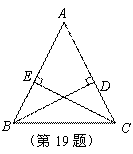

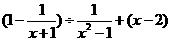 ,其中
,其中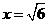 .
.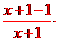 (x+1)(x-1)+(x-2)
(x+1)(x-1)+(x-2)