0 48111 48119 48125 48129 48135 48137 48141 48147 48149 48155 48161 48165 48167 48171 48177 48179 48185 48189 48191 48195 48197 48201 48203 48205 48206 48207 48209 48210 48211 48213 48215 48219 48221 48225 48227 48231 48237 48239 48245 48249 48251 48255 48261 48267 48269 48275 48279 48281 48287 48291 48297 48305 447348
 ,则
,则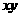 的值为
的值为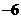
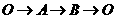 D路径散步,能近似地刻画小明到出发点O的距离y与时间x之间的函数图象是
D路径散步,能近似地刻画小明到出发点O的距离y与时间x之间的函数图象是
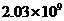 B.
B.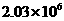 C.
C.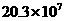 D.
D.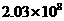
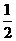 B.
B.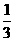 C.
C. D.
D.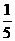
 A.
A.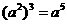 B.
B.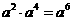 C.
C.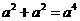 D.
D.
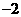 的绝对值是
的绝对值是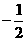 B.2 C.
B.2 C.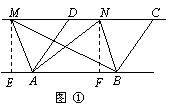 ∵ AD∥BC,AD=BC,
∵ AD∥BC,AD=BC,  S△ABM=
S△ABM= ,S△ABN=
,S△ABN=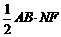 ,
, 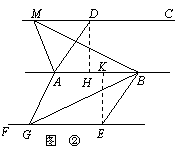 则∠DHA=∠EKB=90°.
则∠DHA=∠EKB=90°. 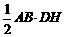 ,S△ABG=
,S△ABG= ,
,  .
. ,解得
,解得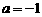 .
. ,即
,即 . ………………………5分
. ………………………5分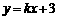 ,代入点A的坐标,得
,代入点A的坐标,得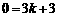 ,解得
,解得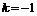 .
.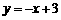 .
. 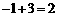 .
. 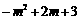 .
. 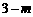 ,EF∥CG.
,EF∥CG.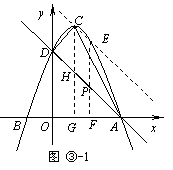 由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等.
由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等. 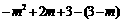 =
=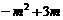 .
. 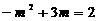 .
. 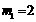 ,
,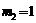 . ……………………………7分
. ……………………………7分 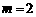 时,PF=3-2=1,EF=1+2=3.
时,PF=3-2=1,EF=1+2=3.
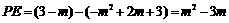 . ……………………………………………9分
. ……………………………………………9分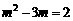 .解得
.解得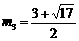 ,
,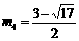 . ………………………………10分
. ………………………………10分 时,E点的纵坐标为
时,E点的纵坐标为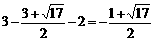 ;
; 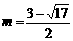 时,E点的纵坐标为
时,E点的纵坐标为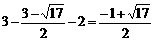 .
. 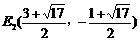 ;
;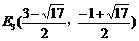 . ………………12分
. ………………12分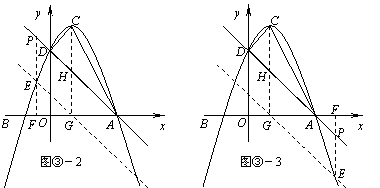
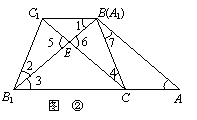 ∴ BC1∥AC.
∴ BC1∥AC.
 理由如下:由题意,知△ABC≌△A1B1C1,
理由如下:由题意,知△ABC≌△A1B1C1, (180°-∠C1BC),∠A=
(180°-∠C1BC),∠A=