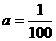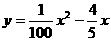7.某商场用36万元购进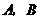 两种商品,销售完后共获利6万元,其进价和售价如下表:
两种商品,销售完后共获利6万元,其进价和售价如下表:
|
|
 |
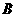 |
|
进价(元/件) |
1200 |
1000 |
|
售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1)该商场购进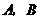 两种商品各多少件;
两种商品各多少件;
(2)商场第二次以原进价购进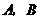 两种商品.购进
两种商品.购进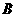 种商品的件数不变,而购进A种商品的件数是第一次的2倍,
种商品的件数不变,而购进A种商品的件数是第一次的2倍, 种商品按原售价出售,而
种商品按原售价出售,而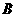 种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,
种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,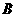 种商品最低售价为每件多少元?
种商品最低售价为每件多少元?
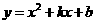 经过点
经过点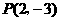 ,
,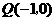 .
. (如图5),与y轴交点为A.求
(如图5),与y轴交点为A.求 的值.
的值. 的面积.
的面积.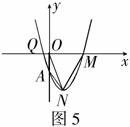
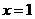 是一元二次方程
是一元二次方程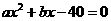 的一个解,且
的一个解,且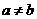 ,求
,求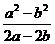 的值.
的值.
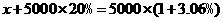
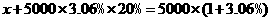
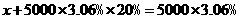
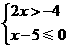 的解集是( )
的解集是( )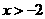 (B)
(B)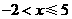
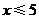 (D)无解
(D)无解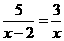 的解为
的解为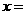 ____________.
____________.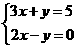 的解是____________.
的解是____________. (1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);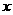 轴,取单位长度为1米,BA的延长方向为
轴,取单位长度为1米,BA的延长方向为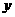 轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。
轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。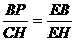 ,即
,即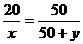 ………①
………①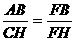 ,即
,即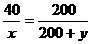 ……②
……②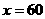 ,
,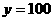

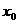 ,
,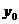 ),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以
),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以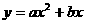 (
(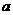 >0),则该抛物线满足
>0),则该抛物线满足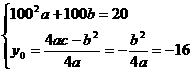
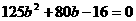
 ,
,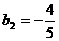
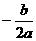 >0,而
>0,而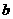 <0,故
<0,故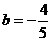 代入前式得:
代入前式得: