9.(•湖北省黄石市)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
A型利润 |
B型利润 |
|
甲店 |
200 |
170 |
|
乙店 |
160 |
150 |
(1)设分配给甲店A型产品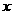 件,这家公司卖出这100件产品的总利润为W(元),求W关于
件,这家公司卖出这100件产品的总利润为W(元),求W关于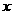 的函数关系式,并求出
的函数关系式,并求出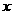 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利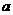 元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
8.(•达州市)“5·12”汶川大地震震惊全世界,面对人类特大灾害,在党中央国务院的领导下,全国人民万众一心,众志成城,抗震救灾.现在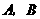 两市各有赈灾物资500吨和300吨,急需运往汶川400吨,运往北川400吨,从
两市各有赈灾物资500吨和300吨,急需运往汶川400吨,运往北川400吨,从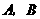 两市运往汶川、北川的耗油量如下表:
两市运往汶川、北川的耗油量如下表:
|
|
汶川(升/吨) |
北川(升/吨) |
|
A市 |
0.5 |
0.8 |
|
B市 |
1.0 |
0.4 |
(1)若从A市运往汶川的赈灾物资为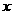 吨,求完成以上运输所需总耗油量y(升)与x(吨)的函数关系式.
吨,求完成以上运输所需总耗油量y(升)与x(吨)的函数关系式.
(2)请你设计一种最佳运输方案,使总耗油量最少,并求出完成以上方案至少需要多少升油?
6.(•重庆市)为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨,、100吨、80吨,需要全部运往四川重灾地区的D、E两县。根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨。
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨。则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
|
|
A地 |
B地 |
C地 |
|
运往D县的费用(元/吨) |
220 |
200 |
200 |
|
运往E县的费用(元/吨) |
250 |
220 |
210 |
为即使将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?














3.(•济南市)某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8∶20~12∶00,下午14∶00~16∶00,每月25元;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品件数与所用时间之间的关系见下表:
|
生产甲产品件数(件) |
生产乙产品件数(件) |
所用总时间(分) |
|
10 |
10 |
350 |
|
30 |
20 |
850 |
信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?










类型之二 借助方程组合或不等式(组)解决方案问题
借助二元一次方程组和一元一次不等式(组)求解方案问题是中考一种新题型,考察了同学们综合运用方程组和不等式深入的分析、比较、归纳和说理的能力.
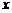 元,水仙花每支
元,水仙花每支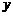 元
元 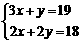 解得:
解得: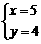
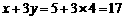
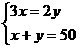 ,解方程组即可。
,解方程组即可。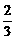 ,但又不少于B种笔记本数量的
,但又不少于B种笔记本数量的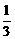 ,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.
,如果设他们买A种笔记本n本,买这两种笔记本共花费w元.