21.(10分)某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
|
|
A |
B |
|
进价(元/件) |
1200 |
1000 |
|
售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
(2007河南省 答案:22.(1)设购进A种商品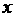 件,B种商品
件,B种商品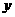 件.
件.
根据题意,得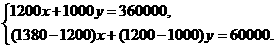
化简,得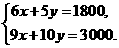
解之,得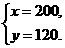
答:该商场购进A、B两种商品分别为200件和120件.
(2)由于A商品购进400件,获利为
(1380-1200)×400 = 72000(元).
从而B商品售完获利应不少于81600-72000 = 9600(元).
设B商品每件售价为x元,则120(x-1000)≥9600.
解之,得x≥1080.
所以,B种商品最低售价为每件1080元.
(本题既对学生学习数学知识与技能的考察,也对学生在数学思考能力和解决问题能力方面作出了要求。)
22某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)对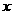 的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
(2007辽宁
答案:24. 解:(1)设按优惠方法①购买需用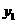 元,按优惠方法②购买需用
元,按优惠方法②购买需用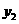 元 1分
元 1分
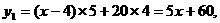
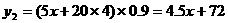 .
·············· 3分
.
·············· 3分
(2)设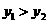 ,即
,即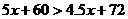 ,
,

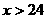 .当
.当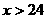 整数时,选择优惠方法②. ············ 5分
整数时,选择优惠方法②. ············ 5分
设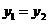 ,∴当
,∴当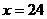 时,选择优惠方法①,②均可.
时,选择优惠方法①,②均可.
∴当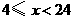 整数时,选择优惠方法①.
··········· 7分
整数时,选择优惠方法①.
··········· 7分
(3)因为需要购买4个书包和12支水性笔,而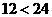 ,
,
购买方案一:用优惠方法①购买,需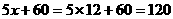 元;····· 8分
元;····· 8分
购买方案二:采用两种购买方式,用优惠方法①购买4个书包,
需要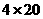 =80元,同时获赠4支水性笔;
=80元,同时获赠4支水性笔;
用优惠方法②购买8支水性笔,需要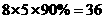 元.
元.
共需80+36=116元.显然116<120. ············· 9分
 最佳购买方案是:
最佳购买方案是:
用优惠方法①购买4个书包,获赠4支水性笔;再用优惠方法②购买8支水性笔.
··············· 10分
(这是一道有关实际生活中的问题,考查了学生的解决实际问题的能力。使学生具有一定的解决问题的基本策略。)
23(本小题满分12分)
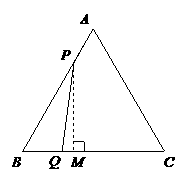
已知:如图,△ABC是边长3cm的等边三角形,动点
P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移
动,它们的速度都是1cm/s,当点P到达点B时,P、Q两
点停止运动.设点P的运动时间为t(s),解答下列问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的
关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出相应的t值;不存在,说明理由;
(2007青岛 答案:
解:⑴ 根据题意:AP=t cm,BQ=t cm.
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t ) cm.
△PBQ中,BP=3-t,BQ=t,
 若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.
当∠BQP=90°时,BQ=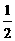 BP.
BP.
即t=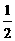 (3-t ),
(3-t ),
t=1 (秒).
当∠BPQ=90°时,BP=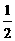 BQ.
BQ.
3-t=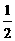 t,
t,
t=2 (秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形. …………………4′
⑵ 过P作PM⊥BC于M .
Rt△BPM中,sin∠B=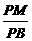 ,
,
∴PM=PB·sin∠B=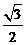 (3-t ).
(3-t ).
∴S△PBQ=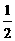 BQ·PM=
BQ·PM=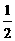 · t ·
· t ·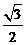 (3-t ).
(3-t ).
∴y=S△ABC-S△PBQ
=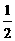 ×32×
×32×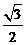 -
-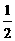 · t ·
· t ·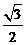 (3-t )
(3-t )
=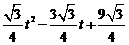 .
.
∴y与t的关系式为: y=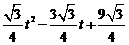 . …………………6′
. …………………6′
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的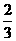 ,
,
则S四边形APQC=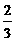 S△ABC .
S△ABC .
∴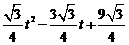 =
=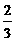 ×
×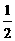 ×32×
×32×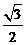 .
.
∴t 2-3 t+3=0.
∵(-3) 2-4×1×3<0,
∴方程无解.
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的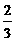 .……8′
.……8′
⑶ 在Rt△PQM中,
MQ=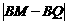 =
=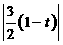 .
.
MQ 2+PM 2=PQ 2.
∴x2=[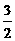 (1-t ) ]2+[
(1-t ) ]2+[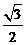 (3-t ) ]2
(3-t ) ]2
=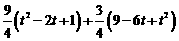
=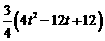 =3t2-9t+9.
……………………………10′
=3t2-9t+9.
……………………………10′
∴t2-3t=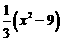 .
.
∵y=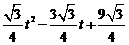 ,
,
∴y=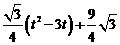 =
=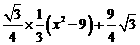 =
=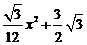 .
.
∴y与x的关系式为:y=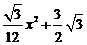 . ……………………………12′
. ……………………………12′
( 本题的目的是考查学生综合运用知识 灵活 合理地选择与运用有关的方法解决实际问题,全面提高学生的解决问题的能力,)
本资料由《七彩教育网》 提供!
 处安装了一台监视器,
处安装了一台监视器, 它的监控角度是
它的监控角度是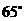 .为了监控整个展厅,最少需在圆形边缘上共安装
.为了监控整个展厅,最少需在圆形边缘上共安装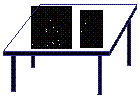

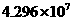 B.
B.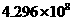 C.
C.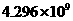 D.
D.

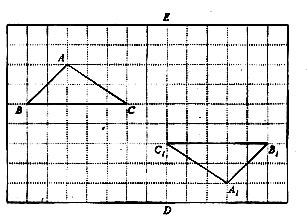 (本小题7分)在如图的方格纸中,每个小正方形的边长都为l, △ABC与△A1B1C1构成的图形是中心对称图形.
(本小题7分)在如图的方格纸中,每个小正方形的边长都为l, △ABC与△A1B1C1构成的图形是中心对称图形.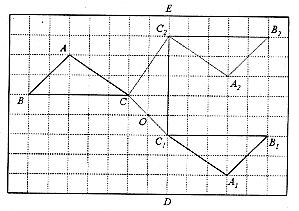 (2006云南省)
(2006云南省)
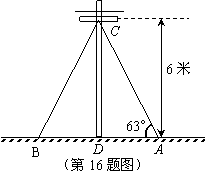 (7分)如图,在电线杆里地面6米高的C处向地面拉缆绳,缆绳
(7分)如图,在电线杆里地面6米高的C处向地面拉缆绳,缆绳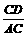 ………………………………………………………………(4分)
………………………………………………………………(4分)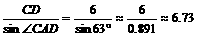 (米) ……………………………(7分)
(米) ……………………………(7分)