0 46489 46497 46503 46507 46513 46515 46519 46525 46527 46533 46539 46543 46545 46549 46555 46557 46563 46567 46569 46573 46575 46579 46581 46583 46584 46585 46587 46588 46589 46591 46593 46597 46599 46603 46605 46609 46615 46617 46623 46627 46629 46633 46639 46645 46647 46653 46657 46659 46665 46669 46675 46683 447348
 走向路灯
走向路灯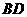 ,当他走到点
,当他走到点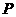 时,发现身后他影子的顶部刚好接触到路灯
时,发现身后他影子的顶部刚好接触到路灯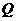 点时,发现身前他影子的顶部刚好接触到路灯
点时,发现身前他影子的顶部刚好接触到路灯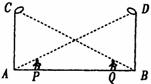
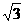 ,(3)△CDE∽△CAB,(4)△CDE的面积与△CAB面积之比为1:4.其中正确的有 ( )
,(3)△CDE∽△CAB,(4)△CDE的面积与△CAB面积之比为1:4.其中正确的有 ( )
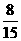 B、 1 C、
B、 1 C、
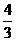 D、
D、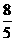

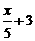 B.
B.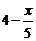 C.
C.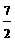 D.
D.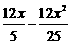
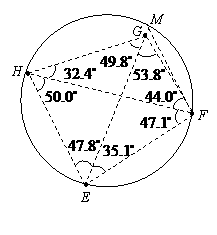 (3)此中转站应建在
(3)此中转站应建在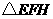 的外接圆圆心处(线段
的外接圆圆心处(线段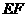 的垂直平分线与线段
的垂直平分线与线段 的垂直平分线的交点处). 10分
的垂直平分线的交点处). 10分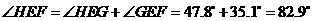 ,
,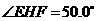 ,
,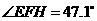 ,
, ,直线
,直线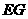 与
与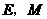 ,
,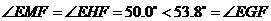 .
.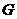 在
在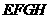 的最小覆盖圆.
的最小覆盖圆.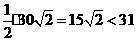 ,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求.
,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求. .将每个装置安装在这些矩形的对角线交点处,设
.将每个装置安装在这些矩形的对角线交点处,设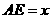 ,则
,则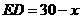 ,
,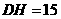 .
.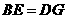 ,得
,得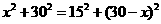 ,
,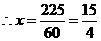 ,
,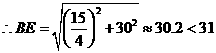 ,
,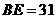 ,
,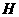 是
是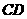 的中点,将每个装置安装在这些矩形的对角线交点处,则
的中点,将每个装置安装在这些矩形的对角线交点处,则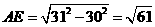 ,
,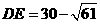 ,
, 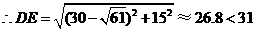 ,即如此安装三个这个转发装置,能达到预设要求.···················································································· (6分)
,即如此安装三个这个转发装置,能达到预设要求.···················································································· (6分)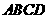 ,设
,设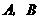 ,
,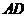 交于
交于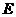 ,连
,连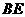 ,则
,则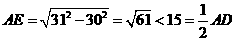 ,这说明用两个直径都为31的圆不能完全覆盖正方形
,这说明用两个直径都为31的圆不能完全覆盖正方形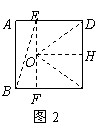
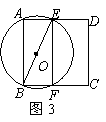
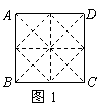
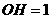 ;
;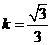 ,
,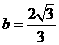 .
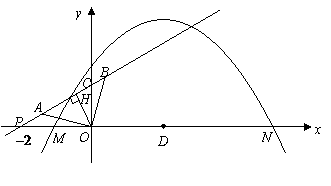
.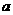 ,使抛物线
,使抛物线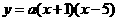 上有一点
上有一点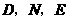 为顶点的三角形与等腰直角
为顶点的三角形与等腰直角 相似.
相似. 以
以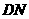 为直角边的等腰直角三角形,另一类是以
为直角边的等腰直角三角形,另一类是以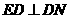 .
.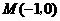 ,
,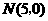 .
.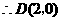 ,
,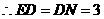 .
.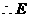 的坐标为
的坐标为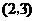 .
. 把
把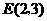 代入抛物线解析式,得
代入抛物线解析式,得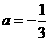 .
.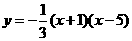 .
.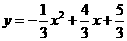 .
.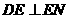 ,
,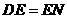 .
.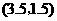 .
.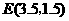 代入抛物线解析式,得
代入抛物线解析式,得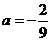 .
.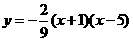 ,即
,即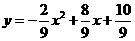
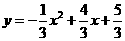 上存在一点
上存在一点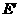 点,那么只有可能
点,那么只有可能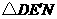 是以
是以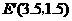 ,显然
,显然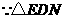 和
和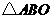 都是等腰直角三角形,
都是等腰直角三角形,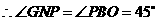 .
.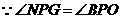 ,
,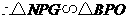 .
.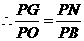 ,
, ,
,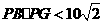 .
.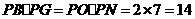 ,
,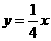 中,得y=-2.
中,得y=-2.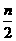 ),C(-2m,-n),E(-m,-n)
),C(-2m,-n),E(-m,-n) =2mn=2k,
=2mn=2k,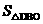 =
=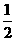 mn=
mn=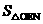 =
=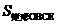 =
=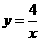 ,得A(4,1),B(-4,-1)
,得A(4,1),B(-4,-1)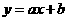 ,由C、M两点在这条直线上,得
,由C、M两点在这条直线上,得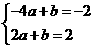 ,解得a=b=
,解得a=b=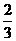
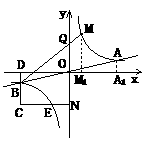
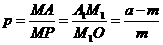 ,
,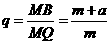
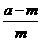 -
-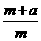 =-2
=-2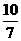
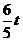
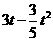
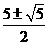
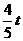
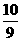
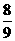 ,BE=
,BE=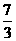
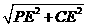 =
=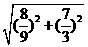 =
=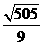
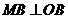 ,
,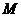 到甲村的最短距离为
到甲村的最短距离为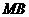 .······································································· (1分)
.······································································· (1分) 点
点 .
.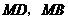 铁路建设的长度之和最小.
铁路建设的长度之和最小.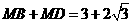 .········································································ (3分)
.········································································ (3分)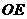 的对称点
的对称点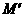 ,则
,则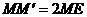 ,连接
,连接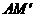 交
交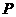 ,则
,则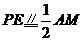 .
.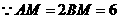 ,
,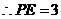 .·········································································· (4分)
.·········································································· (4分)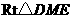 中,
中,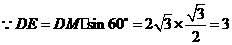 ,
,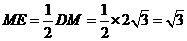 ,
,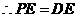 ,
,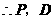 两点重合.即
两点重合.即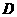 点.············································· (6分)
点.············································· (6分)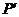 ,连接
,连接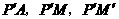 ,则
,则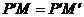 .
.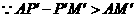 ,
,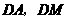 线路铺设的长度之和最小.
线路铺设的长度之和最小.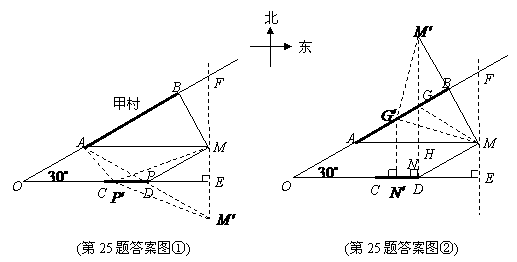 即最小值为
即最小值为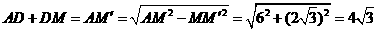 .··········· (7分)
.··········· (7分)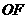 的对称点
的对称点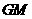 ,则
,则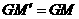 .
.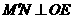 于点
于点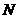 ,交
,交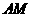 于点
于点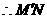 为点
为点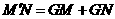 .
.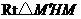 中,
中,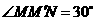 ,
,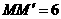 ,
,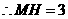 .
.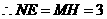 .
.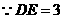 ,
,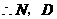 两点重合,即
两点重合,即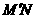 过
过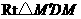 中,
中,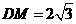 ,
,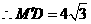 .············································· (10分)
.············································· (10分)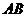 上任取一点
上任取一点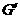 ,过
,过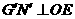 于点
于点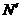 ,连接
,连接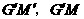 .
.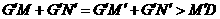 .
.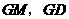 线路铺设的长度之和最小.
线路铺设的长度之和最小.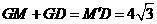 .································································ (11分)
.································································ (11分)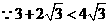 ,
,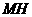 ,
,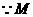 为
为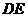 的中点,
的中点,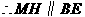 ,
,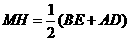 .································· (1分)
.································· (1分)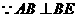 ,
,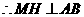 .··········································································· (1分)
.··········································································· (1分)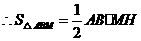 ,得
,得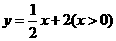 ;······································ (2分)(1分)
;······································ (2分)(1分)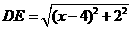 .··································································· (1分)
.··································································· (1分)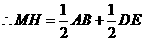 ,即
,即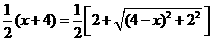 .·························· (2分)
.·························· (2分)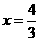 ,即线段
,即线段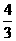 ;······································································· (1分)
;······································································· (1分)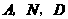 为顶点的三角形与
为顶点的三角形与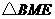 相似,
相似,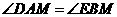 .··············································································· (1分)
.··············································································· (1分)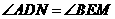 ;②
;②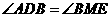 .
.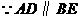 ,
,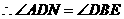 .
.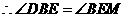 .
.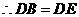 ,易得
,易得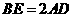 .得
.得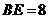 ;······················································· (2分)
;······················································· (2分)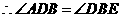 .
.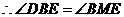 .又
.又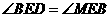 ,
,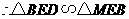 .
.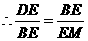 ,即
,即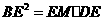 ,得
,得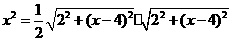 .
.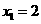 ,
,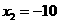 (舍去).即线段
(舍去).即线段