0 46488 46496 46502 46506 46512 46514 46518 46524 46526 46532 46538 46542 46544 46548 46554 46556 46562 46566 46568 46572 46574 46578 46580 46582 46583 46584 46586 46587 46588 46590 46592 46596 46598 46602 46604 46608 46614 46616 46622 46626 46628 46632 46638 46644 46646 46652 46656 46658 46664 46668 46674 46682 447348
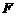 在
在 上,
上, ,
,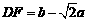 ,
,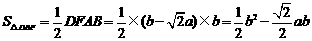 .
.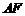 , 由题意易知
, 由题意易知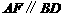 ,
,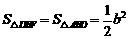 .
.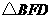 的边
的边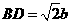 ,故当F点到BD的距离取得最大、最小值时,
,故当F点到BD的距离取得最大、最小值时,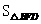 取得最大、最小值.
取得最大、最小值.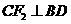 时,
时, 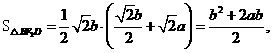
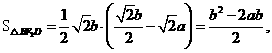
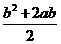 .(如果答案为4a2或b2也可)
.(如果答案为4a2或b2也可)
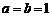 ,
,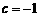 时,抛物线为
时,抛物线为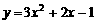 ,
,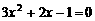 的两个根为
的两个根为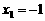 ,
,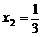 .
. 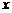 轴公共点的坐标是
轴公共点的坐标是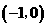 和
和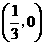 . ················································ 2分
. ················································ 2分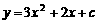 ,且与
,且与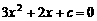 ,判别式
,判别式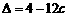 ≥0,有
≥0,有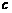 ≤
≤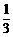 . ········································ 3分
. ········································ 3分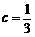 时,由方程
时,由方程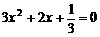 ,解得
,解得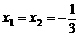 .
.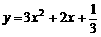 与
与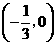 .·································
4分
.·································
4分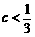 时,
时,  ,
,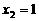 时,
时,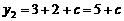 .
.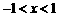 时,该抛物线与
时,该抛物线与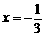 ,
,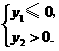 即
即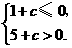
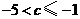 .
.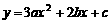 ,
,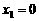 时,
时,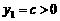 ;
;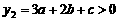 ,
,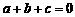 ,∴
,∴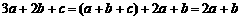 .
.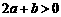 .而
.而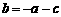 ,∴
,∴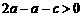 ,即
,即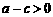 .
.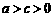 . ············································································································ 7分
. ············································································································ 7分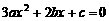 的判别式
的判别式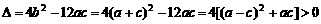 ,
, 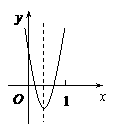 ∴抛物线
∴抛物线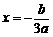 ,
,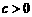 ,
,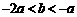 ,
,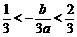 .
.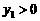 ;
;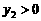 ,观察图象,
,观察图象,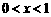 范围内,该抛物线与
范围内,该抛物线与
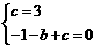 解得
解得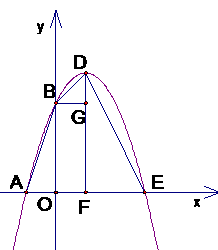 ∴抛物线的线的解析式为
∴抛物线的线的解析式为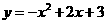



 ,
, 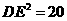 即:
即: 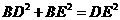 ,所以
,所以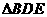 是直角三角形
是直角三角形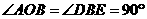 ,且
,且 ,
,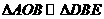 .
.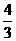 x+2
x+2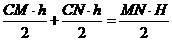
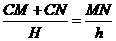
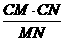
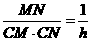
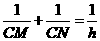
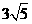 ,sin∠OAB=
,sin∠OAB=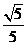 ,
,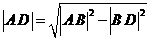
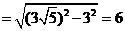
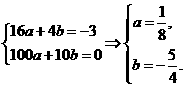
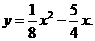 ……2分
……2分 的顶点,
的顶点, x=4或x=6.
x=4或x=6.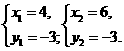
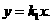
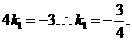
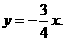
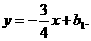
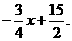
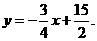
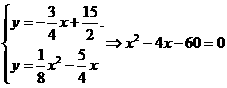 ,即(x-10)(x+6)=0.
,即(x-10)(x+6)=0.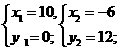
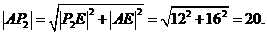
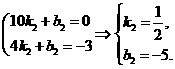
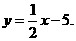
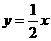
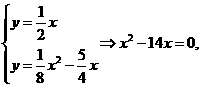 即x(x-14)=0.
即x(x-14)=0.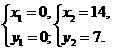
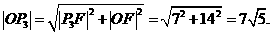
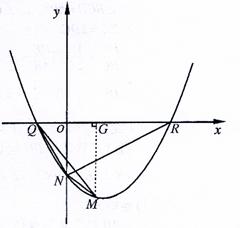 可设抛物线的函数表达式为
可设抛物线的函数表达式为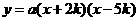 (a>0).
(a>0).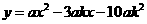
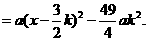
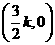 、N(0,-10ak2)、M
、N(0,-10ak2)、M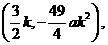
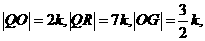
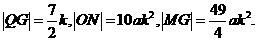
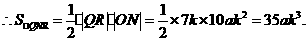
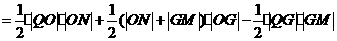
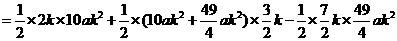
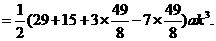
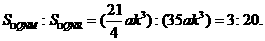 ……2分
……2分 ……1分
……1分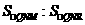 的值为3:20.
……1分
的值为3:20.
……1分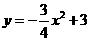 中,令
中,令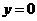
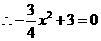
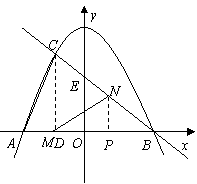
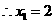 ,
,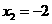
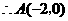 ,
,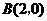 ····················································· 1分
····················································· 1分 点
点 在
在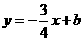 上
上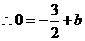
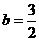
 的解析式为
的解析式为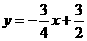 ···················································································· 2分
···················································································· 2分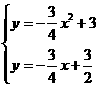 ,得
,得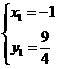
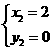 ·························································· 4分
·························································· 4分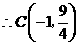 ,
,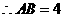 ,
,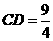 ····································································································· 5分
····································································································· 5分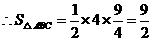 ······························································································· 6分
······························································································· 6分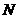 作
作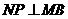 于点
于点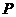
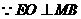
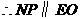
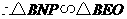 ····································································································· 7分
····································································································· 7分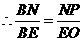 ················································································································ 8分
················································································································ 8分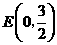
 在
在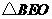 中,
中,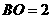 ,
,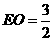 ,则
,则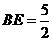
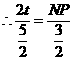 ,
,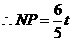 ····························································································· 9分
····························································································· 9分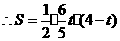
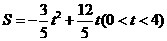 ·························································································· 10分
·························································································· 10分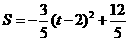 ··································································································· 11分
··································································································· 11分 时,
时,
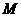 运动2秒时,
运动2秒时, 的面积达到最大,最大为
的面积达到最大,最大为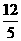 .
.  在
在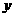 轴上························································································· 1分
轴上························································································· 1分 ,如图所示,在
,如图所示,在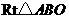 中,
中,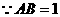 ,
,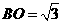 ,
,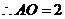
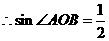 ,
,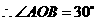
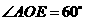
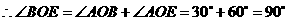
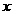 轴上,
轴上,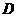 作
作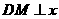 轴于点
轴于点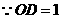 ,
,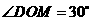
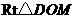 中,
中,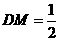 ,
,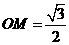
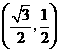 ····························································································· 5分
····························································································· 5分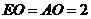 ,点
,点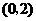
 的坐标为
的坐标为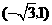 ······························································································· 6分
······························································································· 6分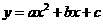 经过点
经过点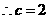
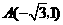 ,
,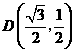 代入
代入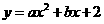 中得
中得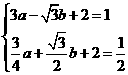 解得
解得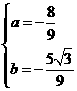
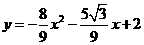 ·························································· 9分
·························································· 9分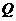 .············································································ 10分
.············································································ 10分 的面积
的面积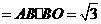
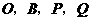 为顶点的平行四边形面积为
为顶点的平行四边形面积为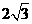 .
.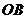 为此平行四边形一边,
为此平行四边形一边,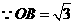
 边上的高为2······································································································ 11分
边上的高为2······································································································ 11分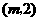
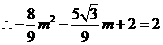
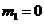 ,
,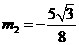
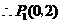 ,
,
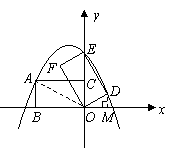
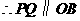 ,
,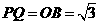 ,
,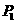 的坐标为
的坐标为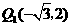 ,
,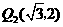 ;
;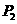 的坐标为
的坐标为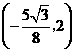 时,
时, ,
,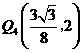 .·················································· 14分
.·················································· 14分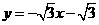 与
与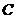 .
.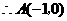 ,
,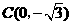 ······························································································· 1分
······························································································· 1分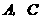 都在抛物线上,
都在抛物线上,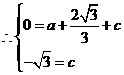
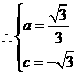
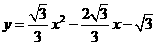 ······························································ 3分
······························································ 3分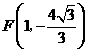 ····································································································· 4分
····································································································· 4分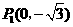 ··················································································································· 7分
··················································································································· 7分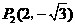 ·················································································································· 9分
·················································································································· 9分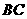 到点
到点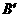 ,使
,使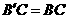 ,连接
,连接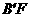 交直线
交直线 于点
于点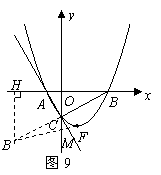 过点
过点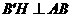 于点
于点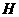 .
.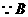 点在抛物线
点在抛物线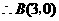
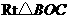 中,
中,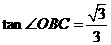 ,
,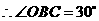 ,
,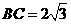 ,
,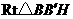 中,
中,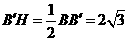 ,
,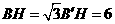 ,
,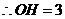 ,
,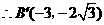 ····················································· 12分
····················································· 12分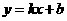
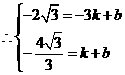 解得
解得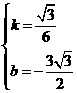
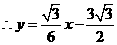 ······································································································ 13分
······································································································ 13分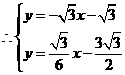 解得
解得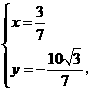

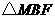 的周长最小,此时
的周长最小,此时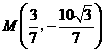 .········· 14分
.········· 14分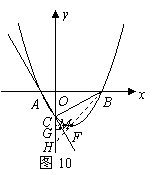 过点
过点 作
作 交
交 轴于点
轴于点 ,则
,则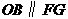 ,
,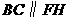 .
.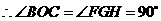 ,
,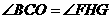
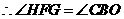
 .
.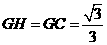 ,
, 为线段
为线段 的垂直平分线,可证得
的垂直平分线,可证得 为等边三角形,
为等边三角形, 垂直平分
垂直平分 .
.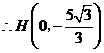 ··················································· 12分
··················································· 12分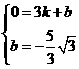 解得
解得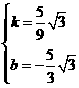
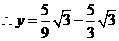 ······································································································ 13分
······································································································ 13分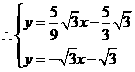 解得
解得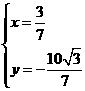
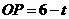 ,
,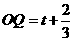 .
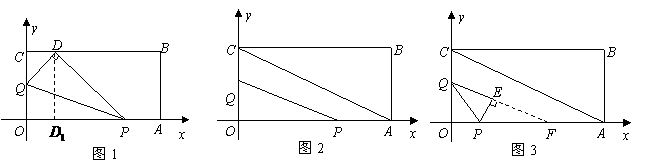
.

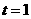 时,过
时,过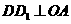 ,交
,交 于
于 ,如图1,
,如图1,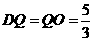 ,
,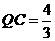 ,
, ,
,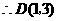 .
.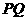 能与
能与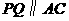 ,如图2,则
,如图2,则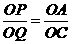 ,
,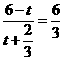 ,
,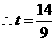 ,而
,而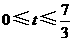 ,
,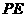 不能与
不能与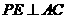 ,延长
,延长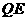 交
交 .
.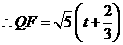 .
.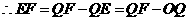

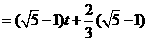 .
.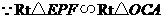 ,
,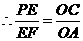 ,
,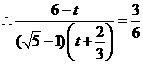 ,
,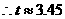 ,而
,而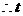 不存在.
不存在.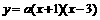 (a≠0)
(a≠0) 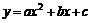 (a≠0)
(a≠0)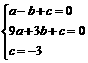 ,解之得:
,解之得: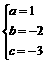
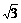
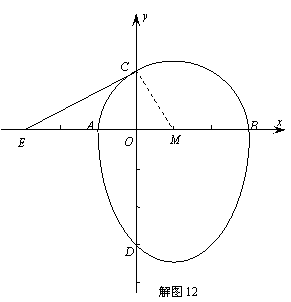 ∴切线CE的解析式为
∴切线CE的解析式为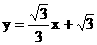 ··························································· 8分
··························································· 8分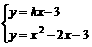 只有一组解
只有一组解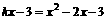 有两个相等实根,∴k=-2············································· 11分
有两个相等实根,∴k=-2············································· 11分