摘要:如图1.操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上.取线段AE的中点M. 探究:线段MD.MF的关系.并加以证明. 说明:(1)如果你经历反复探索.没有找到解决问题的方法.请你把探索过程中的某种思路写出来在你经历说明(1)的过程之后.可以从下列①.②.③中选取一个补充或更换已知条件.完成你的证明. 注意:选取①完成证明得10分,选取②完成证明得7分,选取③完成证明得5分. ① DM的延长线交CE于点N.且AD=NE, ② 将正方形CGEF绕点C逆时针旋转45°. 其他条件不变,③在②的条件下且CF=2AD. 附加题:将正方形CGEF绕点C旋转任意角度后.其他条件不变.探究:线段MD.MF的关系.并加以证明. 例2如图.将一块直角三角形纸板的直角顶点放在处.两直角边分别与轴平行.纸板的另两个顶点恰好是直线与双曲线的交点. (1)求和的值, (2)设双曲线在之间的部分为.让一把三角尺的直角顶点在上 滑动.两直角边始终与坐标轴平行.且与线段交于两点.请探究是否存在点使得.写出你的探究过程和结论. 知识点: 解:(1)∵在双曲线上.∥轴.∥轴. ∴A.B的坐标分别.. 又点A.B在直线上.∴ 解得或 当且时.点A.B的坐标都是.不合题意.应舍去, 当且时.点A.B的坐标分别为,,符合题意. ∴且. (2)假设存在点使得. ∵ ∥轴.∥轴.∴∥. ∴.∴Rt∽Rt,∴, 设点P坐标为(1<x<8=.则M点坐标为. ∴.又. ∴.即 (※) ∵.∴方程(※)无实数根. 所以不存在点使得. 练习二
网址:http://m.1010jiajiao.com/timu3_id_450673[举报]
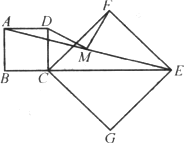
如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
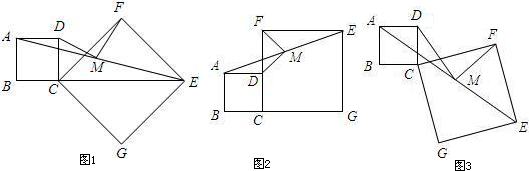
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.

查看习题详情和答案>>
如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.

查看习题详情和答案>>
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.

查看习题详情和答案>>
如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.

查看习题详情和答案>>
探究:线段MD、MF的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得7分;选取③完成证明得5分.
①DM的延长线交CE于点N,且AD=NE;②将正方形CGEF6绕点C逆时针旋转45°(如图),其他条件不变;③在②的条件下,且CF=2AD.
附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.