摘要：解:(1)∵ABCD是矩形.MN∥AD.EF∥CD∴四边形PEAM.PNCF也均为矩形 ∴＝PM·PE＝.＝PN·PF＝ 又∵BD是对角线. ∴△PMB≌△BFP.△PDE≌△DPN.△DBA≌△DBC ∵. ∴＝ ∴ (2)成立.理由如下: ∵ABCD是平行四边形.MN∥AD.EF∥CD ∴四边形PEAM.PNCF也均为平行四边形 仿(1)可证 过E作EH⊥MN于点H.则 ∴ 同理可得 又∵∠MPE＝∠FPN＝∠A ∴ ∴PM·PE＝PN·PF.即 (3)方法1:存在.理由如下: 由(2)可知. 又∵.即.. 而. ∴.即∴. 故存在实数或.使得.
网址：http://m.1010jiajiao.com/timu3_id_450671[举报]
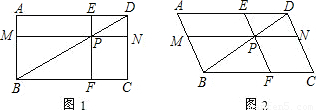
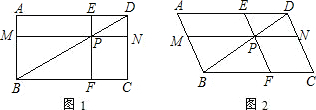
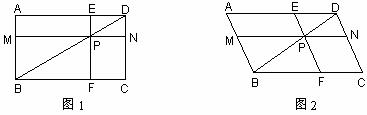
已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设a=PM•PE，b=PN•PF，解答下列问题：
（1）当四边形ABCD是矩形时，见图1，请判断a与b的大小关系，并说明理由；
（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的结论是否成立？并说明理由；
（3）在（2）的条件下，设
=k，是否存在这样的实数k，使得
=
？若存在，请求出满足条件的所有k的值；若不存在，请说明理由．
查看习题详情和答案>>
（1）当四边形ABCD是矩形时，见图1，请判断a与b的大小关系，并说明理由；
（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的结论是否成立？并说明理由；
（3）在（2）的条件下，设
| BP |
| PD |
| S平行四边形PEAM |
| S△ABD |
| 4 |
| 9 |
查看习题详情和答案>>
已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设a=PM•PE，b=PN•PF，解答下列问题：
（1）当四边形ABCD是矩形时，见图1，请判断a与b的大小关系，并说明理由；
（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的结论是否成立？并说明理由；
（3）在（2）的条件下，设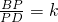
，是否存在这样的实数k，使得
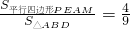？若存在，请求出满足条件的所有k的值；若不存在，请说明理由．
查看习题详情和答案>>
已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设
＝PM?PE，
＝PN?PF，解答下列问题：
（1）当四边形ABCD是矩形时，见图1，请判断与的大小关系，并说明理由；
（2）当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的结论是否成立？并说明理由；
（3）在（2）的条件下，设
，是否存在这样的实数
，使得
？若存在，请求出满足条件的所有的值；若不存在，请说明理由。
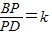，是否存在这样的实数k，使得
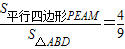？若存在，请求出满足条件的所有k的值；若不存在，请说明理由．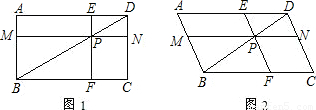
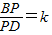，是否存在这样的实数k，使得
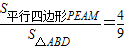？若存在，请求出满足条件的所有k的值；若不存在，请说明理由．