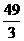2、为了迎接2008年北京奥运会的到来,某足球协会举办了一次足球联赛,其记分规则及奖励方案如下表:
|
|
胜一场 |
平一场 |
负一场 |
|
积 分 |
3 |
1 |
0 |
|
奖金(元/人) |
2000 |
1000 |
0 |
当比赛进行到14轮结束(每队均需比赛14场)时,甲队积分28分,设甲队胜x场,平y场.
⑴用x的代数式表示y;
⑵判断甲队胜、平、负各几场?并说明理由;
⑶若每赛一场,每名参赛队员均得出场费600元。设甲队中一名参赛队员所得的奖金与出场费的和为W(元),试求出W的最大值和最小值。
解:
1、近期,海峡两岸关系的气氛大为改善。大陆相关部门于2005年8月1日起对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售。某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
|
每千克售价(元) |
50 |
49 |
48 |
47 |
46 |
… |
|
每天销量(千克) |
40 |
42 |
44 |
46 |
48 |
… |
设当单价从50元/千克下调了 元时,销售量为
元时,销售量为 千克;
千克;
(1)写出 与
与 间的函数关系式;
间的函数关系式;
(2)如果凤梨的进价是20元/千克,当该经销商把售价定为多少元时,他能获得日最大利润?
(3)目前两岸还未直接通航,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,问一次进货最多只能是多少千克?
解:
22.(1)
|
传球次数n |
1 |
2 |
3 |
4 |
… |
|
球回到甲手中的概率 |
0 |
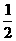 |
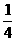 |
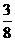 |
|
|
球回到乙手中的概率 |
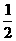 |
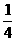 |
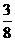 |
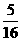 |
|
|
球回到乙手中的概率 |
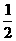 |
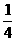 |
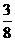 |
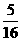 |
|
(2)猜想:当n为奇数时,P(球回到甲手中)<P(球回到乙手中)=P(球回到丙手中)
当n为偶数时,P(球回到甲手中)>P(球回到乙手中)=P(球回到丙手中)
且第n次传球后球回到甲手中的概率与第n-1次传球后球回到乙或丙手中的概率相等(n>1)。
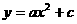 的形式.请根据所给的数据求出
的形式.请根据所给的数据求出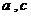 的值.
的值.
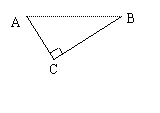 方案②:把它折成横截面为等腰梯形的水槽(如图2).
方案②:把它折成横截面为等腰梯形的水槽(如图2).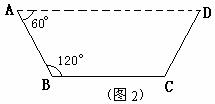 若∠ABC=120°,请你求出该水槽的横截面面积的最大值,
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,
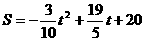 ,当t=
,当t=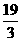 时,S有最大值 ,点P的坐标为(
时,S有最大值 ,点P的坐标为(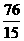 ,
,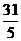 )
)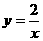 (1≤x≤2)
(1≤x≤2)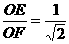 =
=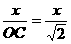 ∴x=1
∴x=1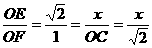 ∴x=2
∴x=2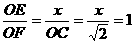 ,∴x=
,∴x=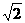
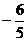 x+3 解析式为y=
x+3 解析式为y=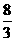 x-
x-