0 446623 446631 446637 446641 446647 446649 446653 446659 446661 446667 446673 446677 446679 446683 446689 446691 446697 446701 446703 446707 446709 446713 446715 446717 446718 446719 446721 446722 446723 446725 446727 446731 446733 446737 446739 446743 446749 446751 446757 446761 446763 446767 446773 446779 446781 446787 446791 446793 446799 446803 446809 446817 447348
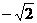 B.2+
B.2+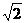 C.2 D.
C.2 D.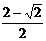
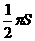 B.
B. C.2
C.2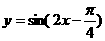 的图象 ( )
的图象 ( ) 个单位 B.向右平移
个单位 B.向右平移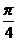 个单位 D.向右平移
个单位 D.向右平移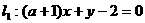 与直线
与直线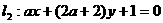 互相垂直,则实数a
互相垂直,则实数a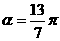 ,则 ( )
,则 ( )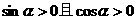 B.
B.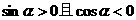
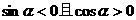 D.
D.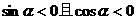
 (本题满分14分)本题共有2个小题,
(本题满分14分)本题共有2个小题, 21.(本满分16分)本题共有3个小题,
21.(本满分16分)本题共有3个小题,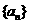 是公方差为
是公方差为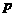 的等方差数列,求
的等方差数列,求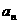 和
和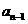
 的关系式;
(2)若数列
的关系式;
(2)若数列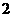 ,公方差为
,公方差为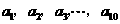 这种顺
这种顺

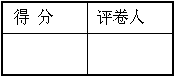 22.(本题满分18分)本题共有3个小题,
22.(本题满分18分)本题共有3个小题,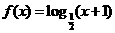 ,当点
,当点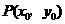 在
在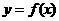 的图像上移动时,
的图像上移动时,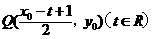 在函数
在函数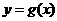 的图像上移动.
的图像上移动.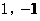 ),点Q也在
),点Q也在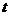 的值;
的值;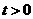 时,试探求一个函数
时,试探求一个函数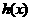 使得
使得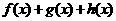 在限定定义域为
在限定定义域为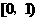 时有最小值而没有最大值.
时有最小值而没有最大值. (本题满分12分)
(本题满分12分)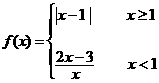 ,解不等式
,解不等式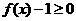 .
.
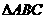 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C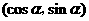 ,
, .
.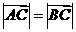 ,求角
,求角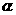 的值;
的值;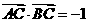 ,求
,求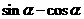 的值.
的值.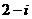 是实系数一元二次方程
是实系数一元二次方程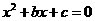
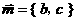 、
、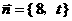 ,求实数
,求实数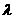
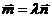 .
.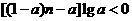 对于任意正整数
对于任意正整数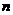 恒成立,则实数
恒成立,则实数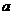 的取值范围是
的取值范围是 . B.
. B.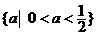 .
.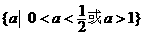 . D.
. D.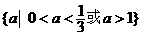 .
.