0 446557 446565 446571 446575 446581 446583 446587 446593 446595 446601 446607 446611 446613 446617 446623 446625 446631 446635 446637 446641 446643 446647 446649 446651 446652 446653 446655 446656 446657 446659 446661 446665 446667 446671 446673 446677 446683 446685 446691 446695 446697 446701 446707 446713 446715 446721 446725 446727 446733 446737 446743 446751 447348
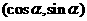 ,b=
,b=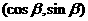 ,且
,且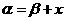 ,
,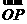 =a + b,
=a + b, = a - b ,记
= a - b ,记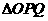 的面积为函数
的面积为函数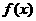 (其中
(其中 为坐标原点) .
为坐标原点) .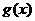 =m
=m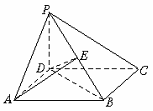 19 (本小题满分12分)
19 (本小题满分12分)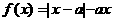 ,其中
,其中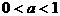 为常数。
为常数。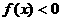 ;
; 是否存在最小值,若存在,求出最小值;若不存在,说明理由。20.(本小题共12分)
是否存在最小值,若存在,求出最小值;若不存在,说明理由。20.(本小题共12分)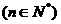 的第2项为8,前10项的和为185。
的第2项为8,前10项的和为185。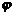 )(w>0,-
)(w>0,-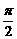 <
<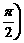 ,给出以下四个论断:
,给出以下四个论断: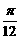 对称;
对称;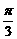 ,0)对称; ④在区间(-
,0)对称; ④在区间(-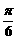 ,0)上是增函数.
,0)上是增函数.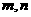 是两条不同的直线,
是两条不同的直线,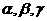 是三个不同的平面,给出下列五个命题:
是三个不同的平面,给出下列五个命题: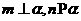 ,则
,则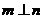 ;②若
;②若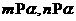 ,则
,则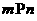 ;③若
;③若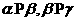 ,
,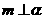 则
则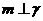 ;④若
;④若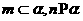 ,
,
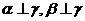 ,则
,则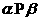 .则以上命题中,是真命题的是 .
.则以上命题中,是真命题的是 .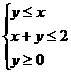 ,那么目标函数
,那么目标函数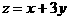 的最大值是______________。
的最大值是______________。 +y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为
+y2=1(a>1)的两个焦点为F1、F2,P为椭圆上一点,且∠F1PF2=60°,则|PF1|·|PF2|的值为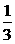 C.
C.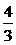 D.
D.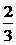
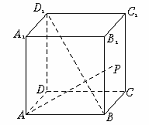
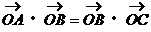 =
=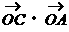 ,则O是△ABC的( )
,则O是△ABC的( ) 是双曲线
是双曲线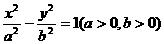 的右准线,以原点为圆心且过双曲线的焦点
的圆,被直线
的右准线,以原点为圆心且过双曲线的焦点
的圆,被直线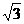 .
(B)
.
(B)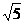 .
(C)
.
(C)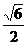 .
(D)
.
(D)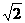 .
.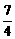 B.
B. C.
C.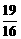 D.
D.