摘要: 已知a=.b=,且,=a + b,= a - b ,记的面积为函数 (其中为坐标原点) . (1)求函数的的表达式; (2) 求函数=m+3的最大值与最小值. 18 如图.四棱锥P-ABCD的底面ABCD为正方形.PD⊥底面ABCD.PD=AD. 求证:(1)平面PAC⊥平面PBD, (2)求PC与平面PBD所成的角, (3)在线段PB上是否存在一点E.使得PC⊥平面ADE?若存在.请加以证明.并求此时二面角A-ED-B的大小,若不存在.请说明理由. 19 设函数.其中为常数. (I)解不等式, (II)试推断函数是否存在最小值.若存在.求出最小值,若不存在.说明理由.20. 已知等差数列{an}的第2项为8.前10项的和为185. (I)求数列{an}的通项公式, (II)若从数列{an}中依次取出第2项.第4项.第8项.-.第2n项.-.按取出顺序组成一个新数列{bn}.试求数列{bn}的前n项和Sn, (III)设Tn=n(9+an).试比较Sn与Tn的大小.并说明理由. 试推断函数是否存在最小值.若存在.求出最小值,若不存在.说明理由.
网址:http://m.1010jiajiao.com/timu3_id_4466550[举报]
(本小题满分12分)
已知a=(1,2), b=(-2,1),x=a+![]() b,y=-ka+
b,y=-ka+![]() b (k
b (k![]() R).
R).
(1)若t=1,且x∥y,求k的值;
(2)若t![]() R +,x?y=5,求证k≥1.
R +,x?y=5,求证k≥1.
(本小题满分12分) 已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点,且PC⊥AB. (Ⅰ)求二面角P-AC-B的正切值; (Ⅱ)求点B到平面PAC的距离.
查看习题详情和答案>>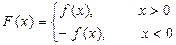 ,
,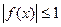 在区间(0,1]上恒成立,试求b的取值范围。
在区间(0,1]上恒成立,试求b的取值范围。 成等差数列.
成等差数列.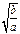 与
与 的大小,并证明你的结论;
的大小,并证明你的结论;