摘要：已知定义域为R的二次函数的最小值为0且有.直线被的图像截得的弦长为.数列满足.. (1)求函数, (2)求数列的通项公式, (3)设.求数列的最值及相应的n. (1)解:设.则直线与图象的两个交点为(1.0). ---------2分 -------4分 (2) ----6分 数列是首项为1.公比为的等比数列----8分 ----9分 (3) 令 ----10分 则 .的值分别为--.经比较距最近----12分 ∴当时.有最小值是. ------------13分 当时.有最大值是0. -------------14分
网址：http://m.1010jiajiao.com/timu3_id_4459466[举报]
已知定义域为R的二次函数f（x）的最小值为0且有f（1+x）=f（1-x），直线g（x）=4（x-1）被f（x）的图象截得的弦长为4
，数列{an}满足，（an+1-an）g（an）+f（an）=0（n∈N*）．
（I）求函数f（x）；
（II）求数列{an}的通项公式；
（III）设bn=
，(n∈N*)，求数列{bn}的前n项和Tn．
查看习题详情和答案>>
| 17 |
（I）求函数f（x）；
（II）求数列{an}的通项公式；
（III）设bn=
| (an-1)g(n) |
| 4 |
，直线
图象截得的弦长为
，数列
，
的通项公式；
的最值及相应的n.
已知定义域为R的二次函数f（x）的最小值为0且有f（1+x）=f（1-x），直线g（x）=4（x-1）被f（x）的图象截得的弦长为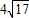
，数列{an}满足，（an+1-an）g（an）+f（an）=0（n∈N*）．
（I）求函数f（x）；
（II）求数列{an}的通项公式；
（III）设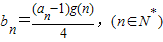
，求数列{bn}的前n项和Tn．
查看习题详情和答案>>
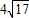，数列{an}满足，（an+1-an）g（an）+f（an）=0（n∈N*）．（I）求函数f（x）；
（II）求数列{an}的通项公式；
（III）设
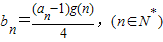，求数列{bn}的前n项和Tn．查看习题详情和答案>>
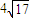，数列{an}满足，（an+1-an）g（an）+f（an）=0（n∈N*）．
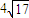，数列{an}满足，（an+1-an）g（an）+f（an）=0（n∈N*）．