摘要:文16. 已知..求和的值. [考查目标]本小题主要考查三角函数的诱导公式及和(差)角公式等基础知识. 考查运算能力. [答卷分析] 平均分:10.11 难度:0.84 标准差:3.74 [本题别解主要有] 别解: 令.则r=5k,y=3k .又由 得:x=±4k. 而.所以x=4k . . [本题出现的典型错误有] ① 公式记错, 例如等. ② 应用万能公式,但公式记不牢. 理16. 已知. (Ⅰ)求的值, (Ⅱ)求的值. [考查目标]本小题主要考查三角函数的诱导公式及和(差)角公式等基础知识. 考查运算能力. [命题溯源]P125.练习1(1)改编. [本题别解主要有] 别解一: 别解二:. 又可知 . 从 ∴. [答卷分析] 平均分:9.55 难度:0.80 标准差:3.71 [本题出现的典型错误有] ① 从而 ② 由.则:, 知可在第二或四象限. 当在第二:; 当在第四:. 文17. 如图6所示.在长方体中. .连结 .. (Ⅰ)求证:, (Ⅱ)求三棱锥的体积. 图6 [考查目标]本小题主要考查空间线面关系.考查空间想象能力和推理运算能力. [答卷分析] 平均分:10.11 难度:0.73 标准差:4.75 [本题别解主要有] ① 用三垂线定理证明(略); ② 先证 .正方形ABCD中.. ③ 向量法. 以A为原点.AB.AD.AA1所在直线分别为x轴.y轴建立空间直角坐标系. 则B ,A1 . [本题出现的典型错误有] ① 叙述不规范:如“ 写成“ 等; ② 建立直角坐标系.但叙述不完整.或图形上不标方向; ③ 书写不规范; ④ 用等积法求.但找错高.常把OC当作三棱锥的高; ⑤ 计算时.将作为三棱锥的高; ⑥ 计算出错. 理17. 如图5所示.在长方体中. .是棱上的点. 且. (Ⅰ)求三棱锥的体积, (Ⅱ)求证:平面. [考查目标]本小题主要考查空间线面关系.考查空间想象能 力和推理运算能力. [答卷分析] 平均分:11.60 难度:0.80 标准差:3.41. [本题别解主要有] 别解:(Ⅰ)平面BDE的法向量. 点C到平面BDE的距离d=,SBDE=,再计算体积. (Ⅱ)∵∴ ∴ ∴AC⊥平面BDE. [本题出现的典型错误有] ① 第(Ⅰ)问.没有交待高CE扣1分 , ② 第(Ⅱ)问.和的运算过程没有造成扣分, ③ 向量垂直 没有转化为直线垂直A1C⊥BD, A1C⊥BE造成扣分. ④ 体积公式记错, 如,等. 文18. 函数和的图像的示意图如图7所示. 设两函数的图像交于点..且. (Ⅰ)请指出示意图中曲线.分别对应哪一个函数? (Ⅱ)若..且 . 指出.的值.并说明理由, (Ⅲ)结合函数图像的示意图.判断... 的大小.并按从小到大的顺序排列. [考查目标]本小题主要考查空间线面关系.考查空间想象能力和推理运算能力. [答卷分析] 平均分:6.49 难度:0.46 标准差:3.79 [本题别解主要有]观察下表可以得到解答: x 1 2 3 4 5 6 7 8 9 10 G(x) 1 8 17 64 125 216 343 512 729 100 F(x) 2 4 8 16 32 64 128 256 512 1024 [本题出现的典型错误有] (1) ∴ a=1 , b=6 ∵ f, ,符合题意 ∵ .∴ ∴ 当x=1时.离等于的机会较小,当x=2时.离等于2的机会较大, 当x=3时.离等于3的机会较大,-- 当x=10时.离等于10的机会较大,当x=12时.离等于12的机会较小, ∴ 综上所述. ∴ a=2,b=9 令F(x)=, ∵x∈[1,3],根据二分法得.F<0, ∴a=1. (2) 函数符号表达不清楚; (3) 得分点把握不到位:如 ① 计算出f的值,但没有结论f ②f的比较说理不清楚或者没有说理过程 (4) 对“a=1,b=9 的理解不清,不会将问题进行转化,审题缺乏灵活性. 理18. 甲箱的产品中有5个正品和3个次品. 乙箱的产品中有4个正品和3个次品. (Ⅰ)从甲箱中任取2个产品.求这2个产品都是次品的概率, (Ⅱ)若从甲箱中任取2个产品放入乙箱中. 然后再从乙箱中任取一个产品.求取出的这个产品是正品的概率. [考查目标]本小题主要考查条件概率和互斥事件的概率计算.考查运用概率知识解决实 际问题能力. [答卷分析] 平均分:7.65 难度:0.64 标准差:3.81 [本题别解主要有] 别解1:分3类.然后相加而得.解法如下: 记“从甲箱中取出2个产品为正品放入乙箱.然后再从乙箱中取出正品 为事件A. 则P(A)= 记“从甲箱中取出2个产品为一个正品和一个次品放入乙箱.然后再从乙箱中取出正品 为事件B.则P(B)= 记“从甲箱中取出2个产品为次品放入乙箱.然后再从乙箱中取出正品 为事件C. 则P(C)= 记“从乙箱中取出的产品为正品 为事件D.则A.B.C互斥.且D=A+B+C. 所以.P= + + = 别解2:设从甲箱中取了2个产品放入乙箱后.乙箱中的正品数为X.则X的取值可能为4. 5.6.其中 X=4 表示“从甲箱中取出2个产品为次品放入乙箱 .则P(X=4)= “X=5 表示“从甲箱中取出2个产品为一个正品和一个次品放入乙箱 . 则P(X=5)= “X=6 表示“从甲箱中取出2个产品为2个正品放入乙箱 .则P(X=6)= 所以.乙箱中正品数X的期望为 E(X)= 所以.此时从乙箱中再取出一个产品为正品的概率为P = 别解3:(Ⅱ)用表示从甲箱中取出正品数,则的分布列为: 0 1 2 P 故从乙箱中取出一个产品是正品的概率为P=. [本题出现的典型错误有] (1) 概念不清晰 ② 学生对条件概率,互斥事件等基本慨念不清楚; ②甚至有的学生出现等明显问题,体现出学生基本慨念的薄弱; ③少数学生还出现这样的形式. (2) 计算不准确 ①组合数计算==56等低级错误; ②分数相加等. (3) 答题不规范 ①没有必要的文字说明; ③ 运算结果不追求最简,如:等不化简; ③ 第2问很多只考虑了“乙箱中取到正品 的概率.而未注意“甲箱中取来的正品 产生的影响, ④ 忘记作答.扣1分. 文19. 某工厂日生产某种产品最多不超过30件.且在生产过程中次品率与日产量() 件间的关系为 每生产一件正品盈利2900元.每出现一件次品亏损1100元. (Ⅰ)将日利润(元)表示为日产量(件)的函数, (Ⅱ)该厂的日产量为多少件时,日利润最大? () [考查目标]本小题主要考查函数和导数的应用.考查综合运用数学知识分析问题与解决实际问题的能力. [答卷分析] 平均分:1.80 难度:0.15 标准差:2.97 [本题出现的典型错误有]1. 最大问题是计算问题: ① 列出表达式化简错误; ② 求最大值计算不正确. 如: (a)当在 学生知道超出x的范围.但都没有明确交待就直接在x=15处取得最大值3300元 (b)当时.会求导得x=25时.y’=0.但没有明确单调性.直接在x=25时取最大值. (c)没有比较两段函数的最大值.
网址:http://m.1010jiajiao.com/timu3_id_4458488[举报]
|
已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==![]() ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
|
已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==![]() ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数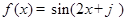 和
和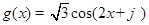 .
.
(Ⅰ)设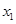 是
是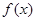 的极大值点,
的极大值点,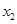 是
是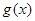 的极小值点,求
的极小值点,求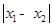 的最小值;
的最小值;
(Ⅱ)若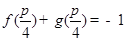 ,且
,且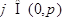 ,求
,求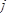 的值.
的值.
查看习题详情和答案>>


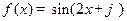 和
和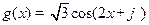 .
.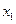 是
是 的极大值点,
的极大值点, 是
是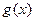 的极小值点,求
的极小值点,求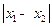 的最小值;
的最小值; ,且
,且 ,求
,求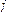 的值.
的值.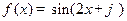 和
和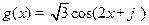 .
.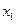 是
是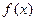 的极大值点,
的极大值点,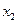 是
是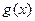 的极小值点,求
的极小值点,求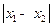 的最小值;
的最小值;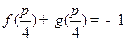 ,且
,且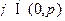 ,求
,求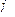 的值.
的值.