摘要:19.解:①函数的图象关于原点对称 对任意实数.有 -------------3分 即恒成立 时.取极小值.且. ----------------------------5分 ②当时.图象上不存在这样的两点使结论成立. 假设图象上存在两点.使得过此两点处的切线互相垂直.则由知两点处的切线斜率分别为----------------- -6分 且 (*) [-1.1]与(*)矛盾------------9分 ③ 令得. 或时. . 时 在[-1.1]上是减函数.且----------11分 在[-1.1]上 时.------14分 20已知数列的前项和为.对一切正整数.点都在函数的图象上.且过点的切线的斜率为. (Ⅰ)求数列的通项公式, (Ⅱ)若.求数列的前项和为, (Ⅲ)设..等差数列的任一项.其中是中的最小数..求的通项公式.
网址:http://m.1010jiajiao.com/timu3_id_4458145[举报]
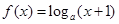 ,若函数
,若函数 的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数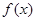 的图象:
的图象: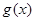 的解析式
的解析式 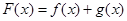 ,讨论
,讨论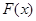 的单调性
的单调性 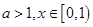 时,总有
时,总有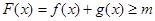 成立,求实数
成立,求实数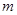 的取值范围。
的取值范围。 ,若函数
,若函数 的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数 的图象:
的图象: 的解析式
的解析式  ,讨论
,讨论 的单调性
的单调性  时,总有
时,总有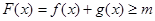 成立,求实数
成立,求实数 的取值范围。
的取值范围。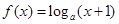 ,若函数
,若函数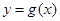 的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数 的图象:
的图象: 的解析式
的解析式 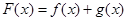 ,讨论
,讨论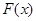 的单调性
的单调性 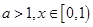 时,总有
时,总有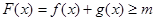 成立,求实数
成立,求实数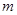 的取值范围。
的取值范围。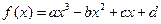 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值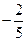 .
.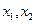 ∈[-1,1],不等式
∈[-1,1],不等式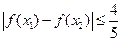 成立;
成立;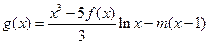 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.