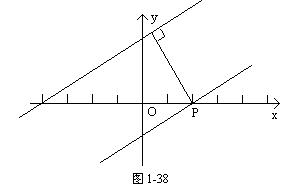
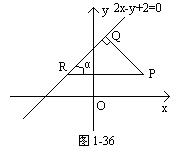
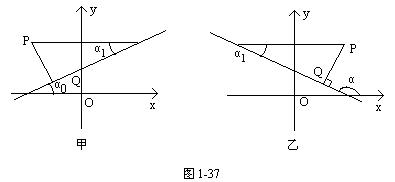
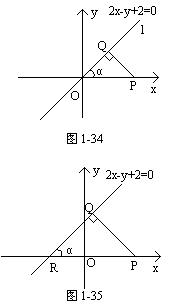
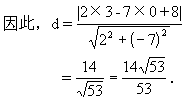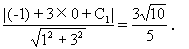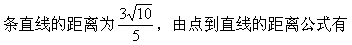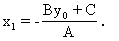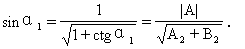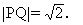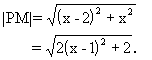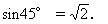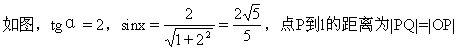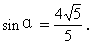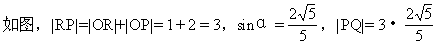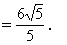0 445212 445220 445226 445230 445236 445238 445242 445248 445250 445256 445262 445266 445268 445272 445278 445280 445286 445290 445292 445296 445298 445302 445304 445306 445307 445308 445310 445311 445312 445314 445316 445320 445322 445326 445328 445332 445338 445340 445346 445350 445352 445356 445362 445368 445370 445376 445380 445382 445388 445392 445398 445406 447348