0 445260 445268 445274 445278 445284 445286 445290 445296 445298 445304 445310 445314 445316 445320 445326 445328 445334 445338 445340 445344 445346 445350 445352 445354 445355 445356 445358 445359 445360 445362 445364 445368 445370 445374 445376 445380 445386 445388 445394 445398 445400 445404 445410 445416 445418 445424 445428 445430 445436 445440 445446 445454 447348
 (B)
(B)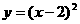 (C)
(C)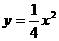 (D)
(D)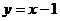
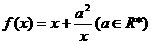 在区间
在区间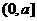 上单调递减
上单调递减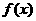 是R上的偶函数,当
是R上的偶函数,当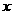 ≥0时,
≥0时,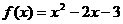 。
(1)用分段函数写出函数
。
(1)用分段函数写出函数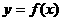 表达式;
(2)利用对称性画出其图象;
(3)指出其单调区间;
(4)利用图象指出在什么区间上
表达式;
(2)利用对称性画出其图象;
(3)指出其单调区间;
(4)利用图象指出在什么区间上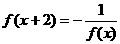 ,若当
,若当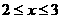 时,
时,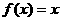 ,则
,则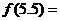 ___.
___. _____.
_____.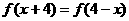 对一切实数x成立,则
对一切实数x成立,则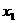 <0,
<0, <0,有
<0,有 ,则
(A)
,则
(A)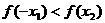 (B)
(B)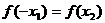 (C)
(C)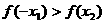 (D)
(D)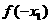 与
与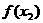 关系不确定
关系不确定