14、(2005年南通)海门市三星镇的叠石桥国际家纺城是全国最大的家纺专业市场,年销售额突破百亿元.2005年5月20日,该家纺城的羽绒被和羊毛被这两种产品的销售价如下表:
|
品 名 |
规格(米) |
销售价(元/条) |
|
羽绒被 |
2×2.3 |
415 |
|
羊毛被 |
2×2.3 |
150 |
现购买这两种产品共80条,付款总额不超过2万元.问最多可购买羽绒被多少条?
解:设购买羽绒被x条,则购买羊毛被(80-x)条,
根据题意,得 415x+150(80-x)≤20000.整理,得 265x≤8000.解之,得 x≤ .∵x为整数,∴x的最大整数值为30.
.∵x为整数,∴x的最大整数值为30.
11、(2005年南安调研)南泉汽车租赁公司共有30辆出租汽车,其中甲型汽车20辆,乙型汽车10辆。现将这30辆汽车租赁给A、B两地的旅游公司,其中20辆派往A地,10辆派往B地,两地旅游公司与汽车租赁公司商定每天价格如下表:
|
|
每辆甲型车租金(元/天) |
每辆乙型车租金(元/天) |
|
A地 |
1000 |
800 |
|
B地 |
900 |
600 |
(1)
设派往A地的乙型汽车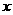 辆,租赁公司这30辆汽车一天共获得的租金为
辆,租赁公司这30辆汽车一天共获得的租金为 (元),求
(元),求 与
与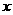 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量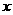 的取值范围;
的取值范围;
(2)若要使租赁公司这30辆汽车一天所获得的租金总额不低于26800元,请你说明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这30辆汽车每天获得的租金最多,请你为租赁公司提出合理的分派方案.
解:(1)
(2)依题意得: ,又因为
,又因为
∴ ,因为
,因为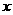 是整数
是整数
∴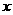 =8,9,10,方案有3种
=8,9,10,方案有3种
方案1:A地派甲型车12辆,乙型车8辆;B地派甲型车8辆,乙型车2辆;
方案2:A地派甲型车11辆,乙型车9辆;B地派甲型车9辆,乙型车1辆;
方案3:A地派甲型车10辆,乙型车10辆;B地派甲型车10辆。
(3)∵ 是一次函数,且
是一次函数,且 ﹥0,
﹥0,
∴ 随
随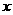 的增大而增大,
的增大而增大,
∴当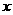 =10时,这30辆车每天获得的租金最多,
=10时,这30辆车每天获得的租金最多,
∴合理的分配方案是A地派甲型车10辆,乙型车10辆;B地派甲型车10辆。


 解不等式(1)得x<14
解不等式(1)得x<14


 ,
, ,
, 
 (浙江省2005)一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2.求x的取值范围.
(浙江省2005)一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2.求x的取值范围. 解这个不等式组,得
解这个不等式组,得
