0 139133 139141 139147 139151 139157 139159 139163 139169 139171 139177 139183 139187 139189 139193 139199 139201 139207 139211 139213 139217 139219 139223 139225 139227 139228 139229 139231 139232 139233 139235 139237 139241 139243 139247 139249 139253 139259 139261 139267 139271 139273 139277 139283 139289 139291 139297 139301 139303 139309 139313 139319 139327 447348
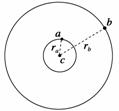 如图4-3-13所示,三个质点a、b、c质量分别为m1、m2、M(M
如图4-3-13所示,三个质点a、b、c质量分别为m1、m2、M(M 答案:1∶8 14
答案:1∶8 14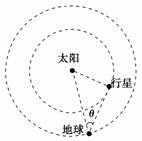 道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地
道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地 如图4-3-11所示,美国空军X-37B无人航天飞机于2010年4月
如图4-3-11所示,美国空军X-37B无人航天飞机于2010年4月 为绕地球沿椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为
为绕地球沿椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为 答案:C
答案:C 答案:A
答案:A