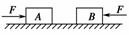
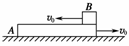
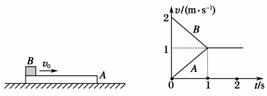
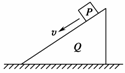
0 139138 139146 139152 139156 139162 139164 139168 139174 139176 139182 139188 139192 139194 139198 139204 139206 139212 139216 139218 139222 139224 139228 139230 139232 139233 139234 139236 139237 139238 139240 139242 139246 139248 139252 139254 139258 139264 139266 139272 139276 139278 139282 139288 139294 139296 139302 139306 139308 139314 139318 139324 139332 447348