0 138625 138633 138639 138643 138649 138651 138655 138661 138663 138669 138675 138679 138681 138685 138691 138693 138699 138703 138705 138709 138711 138715 138717 138719 138720 138721 138723 138724 138725 138727 138729 138733 138735 138739 138741 138745 138751 138753 138759 138763 138765 138769 138775 138781 138783 138789 138793 138795 138801 138805 138811 138819 447348
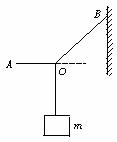 如图所示,绳OA、OB悬挂重物于O点,开始时OA水平.现缓慢提起A端而O点的位置保持不变,则
如图所示,绳OA、OB悬挂重物于O点,开始时OA水平.现缓慢提起A端而O点的位置保持不变,则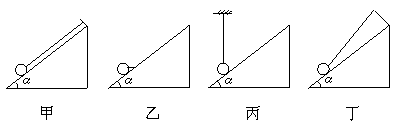
 D.球对斜面压力最大的是丁图所示情况
D.球对斜面压力最大的是丁图所示情况 如图所示,物块P与Q间的滑动摩擦力为5
N,Q与地面间的滑动摩擦力为10
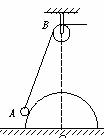
N,R为定滑轮,其质量及摩擦均可忽略不计,现用一水平拉力F作用于P上并使P、Q发生运动,则F至少为
如图所示,物块P与Q间的滑动摩擦力为5
N,Q与地面间的滑动摩擦力为10
N,R为定滑轮,其质量及摩擦均可忽略不计,现用一水平拉力F作用于P上并使P、Q发生运动,则F至少为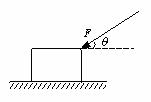 如图所示,一个重为G的木箱放在水平地面上,木箱与水平面间的动摩擦因数为μ,用一个与水平方向成θ角的推力F推动木箱沿地面做匀速直线运动,则推力的水平分力等于
如图所示,一个重为G的木箱放在水平地面上,木箱与水平面间的动摩擦因数为μ,用一个与水平方向成θ角的推力F推动木箱沿地面做匀速直线运动,则推力的水平分力等于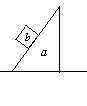 C.μG/(1-μtanθ) D.Fsinθ
C.μG/(1-μtanθ) D.Fsinθ
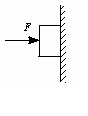 D.两砖之间没有相互挤压的力
D.两砖之间没有相互挤压的力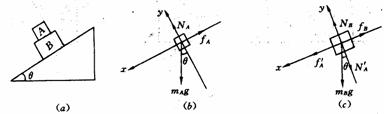 解析:隔离A、B,A受力和坐标轴如图(b)所示,由平衡条件得:
解析:隔离A、B,A受力和坐标轴如图(b)所示,由平衡条件得: 综上所述,本题应选择(B)、(C)、(D)。
综上所述,本题应选择(B)、(C)、(D)。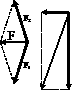 [例8]某压榨机的结构示意图如图,其中B为固定铰链,若在A处作用于壁的力F,则由于力F的作用,使滑块C压紧物块D,设C与D光滑接触,杆的重力不计,求物体D受到的压力大小是F的几倍?(滑块重力不计)
[例8]某压榨机的结构示意图如图,其中B为固定铰链,若在A处作用于壁的力F,则由于力F的作用,使滑块C压紧物块D,设C与D光滑接触,杆的重力不计,求物体D受到的压力大小是F的几倍?(滑块重力不计)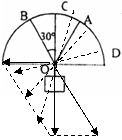 用三角形法则分析力的动态变化
用三角形法则分析力的动态变化 解析:虽然题目问的是挡板AO的受力情况,但若直接以挡板为研究对象,因挡板所受力均为未知力,将无法得出结论.
解析:虽然题目问的是挡板AO的受力情况,但若直接以挡板为研究对象,因挡板所受力均为未知力,将无法得出结论.