0 138636 138644 138650 138654 138660 138662 138666 138672 138674 138680 138686 138690 138692 138696 138702 138704 138710 138714 138716 138720 138722 138726 138728 138730 138731 138732 138734 138735 138736 138738 138740 138744 138746 138750 138752 138756 138762 138764 138770 138774 138776 138780 138786 138792 138794 138800 138804 138806 138812 138816 138822 138830 447348
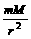 =m
=m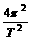 r,由此可得:M=
r,由此可得:M= ;ρ=
;ρ=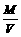 =
=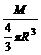 =
=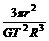 (R为行星的半径)
(R为行星的半径)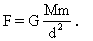
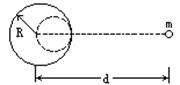 这个引力可以看成是:m挖去球穴后的剩余部分对质点的引力F1与半径为R/2的小球对质点的引力F2之和,即F=F1+F2.因半径为R/2的小球质量M/为
这个引力可以看成是:m挖去球穴后的剩余部分对质点的引力F1与半径为R/2的小球对质点的引力F2之和,即F=F1+F2.因半径为R/2的小球质量M/为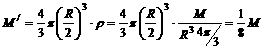 ,
,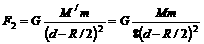
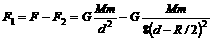
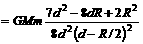
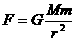 却只能适用于两个质点或均匀球体,挖去球穴后的剩余部分已不再是均匀球了,不能直接使用这个公式计算引力.
却只能适用于两个质点或均匀球体,挖去球穴后的剩余部分已不再是均匀球了,不能直接使用这个公式计算引力.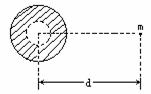 (2)如果题中的球穴挖在大球的正中央,根据同样道理可得剩余部分对球外质点m的引力
(2)如果题中的球穴挖在大球的正中央,根据同样道理可得剩余部分对球外质点m的引力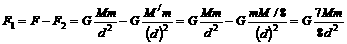
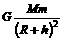 ……② 在地球表面处mg=
……② 在地球表面处mg=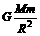 ……③
……③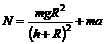 ∴
∴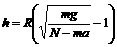 =1.92×104 km.
=1.92×104 km.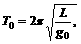
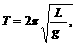 其中l是单摆长度,g0和g分别是两地点的重力加速度。根据万有引力公式得
其中l是单摆长度,g0和g分别是两地点的重力加速度。根据万有引力公式得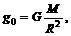
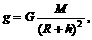 其中G是引力常数,M是地球质量。
其中G是引力常数,M是地球质量。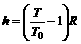
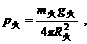
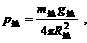 据万有引力公式,火星和地球上的重力加速度分别为
据万有引力公式,火星和地球上的重力加速度分别为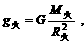
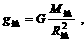
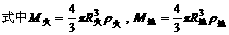 综合上述三式得
综合上述三式得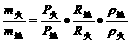
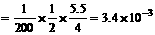
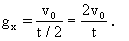 为使物体抛出后不再落回星球表面,应使它所受到的星球引力正好等于物体所需的向心力,即成为卫星发射了出去。
为使物体抛出后不再落回星球表面,应使它所受到的星球引力正好等于物体所需的向心力,即成为卫星发射了出去。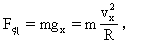
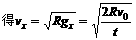 ,这个速度即是这个星球上发射卫星的第一宇宙速度。
,这个速度即是这个星球上发射卫星的第一宇宙速度。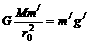 ……①
火星的卫星应满足:
……①
火星的卫星应满足: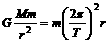 ……②
……②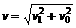 ……④
……④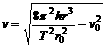
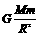 得g=
得g=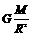 ,由此推得两个不同天体表面重力加速度的关系为
,由此推得两个不同天体表面重力加速度的关系为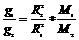
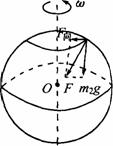 重力是万有引力产生的,由于地球的自转,因而地球表面的物体随地球自转时需要向心力.重力实际上是万有引力的一个分力.另一个分力就是物体随地球自转时需要的向心力,如图所示,由于纬度的变化,物体做圆周运动的向心力F向不断变化,因而表面物体的重力随纬度的变化而变化,即重力加速度g随纬度变化而变化,从赤道到两极逐渐增大.通常的计算中因重力和万有引力相差不大,而认为两者相等,即m2g=G
重力是万有引力产生的,由于地球的自转,因而地球表面的物体随地球自转时需要向心力.重力实际上是万有引力的一个分力.另一个分力就是物体随地球自转时需要的向心力,如图所示,由于纬度的变化,物体做圆周运动的向心力F向不断变化,因而表面物体的重力随纬度的变化而变化,即重力加速度g随纬度变化而变化,从赤道到两极逐渐增大.通常的计算中因重力和万有引力相差不大,而认为两者相等,即m2g=G ,
g=GM/r2常用来计算星球表面重力加速度的大小,在地球的同一纬度处,g随物体离地面高度的增大而减小,即gh=GM/(r+h)2,比较得gh=(
,
g=GM/r2常用来计算星球表面重力加速度的大小,在地球的同一纬度处,g随物体离地面高度的增大而减小,即gh=GM/(r+h)2,比较得gh=(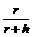 )2·g
)2·g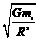 ,比现在地球自转角速度要大得多.
,比现在地球自转角速度要大得多.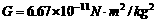 ,称为为有引力恒量。
,称为为有引力恒量。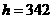 km的圆形轨道。已知地球半径
km的圆形轨道。已知地球半径 km,地面处的重力加速度
km,地面处的重力加速度 。试导出飞船在上述圆轨道上运行的周期T的公式(用h、R、g表示),然后计算周期T的数值(保留两位有效数字)
。试导出飞船在上述圆轨道上运行的周期T的公式(用h、R、g表示),然后计算周期T的数值(保留两位有效数字)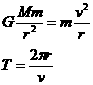
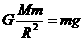
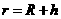
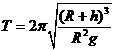

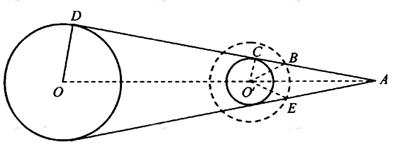
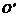 分别表示地球和月球的中心.在卫星轨道平面上,A是地月连心线
分别表示地球和月球的中心.在卫星轨道平面上,A是地月连心线 与地月球表面的公切线ACD的交点,D、C和B分别是该公切线与地球表面、月球表面和卫星轨道的交点.过A点在另一侧作地月球面的公切线,交卫星轨道于E点.卫星在圆弧
与地月球表面的公切线ACD的交点,D、C和B分别是该公切线与地球表面、月球表面和卫星轨道的交点.过A点在另一侧作地月球面的公切线,交卫星轨道于E点.卫星在圆弧 上运动时发出的信号被遮挡.
上运动时发出的信号被遮挡.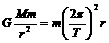 ① (4分)
① (4分)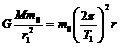 ② (4分)
② (4分)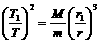 ③
③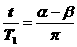 ④ (5分)
④ (5分)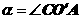 ,
,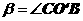 .
.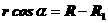 ⑤ (2分)
⑤ (2分)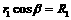 ⑥ (2分)
⑥ (2分)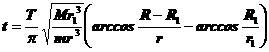 ⑦ (3分)
⑦ (3分)
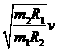 ,
,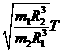 B.
B.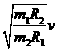 ,
,