2．观察布朗运动时，下列说法中正确的是

A．温度越高，布朗运动越明显

B．大气压强的变化，对布朗运动没有影响

C．悬浮颗粒越大，布朗运动越明显

D．悬浮颗粒的布朗运动，就是构成悬浮颗粒的物质的分子热运动

点评：学生容易出现的错误：认为大气压强的变化对布朗运动会产生影响；把布朗运动和分子热运动混为一谈。

1．如图所示的绝热容器，把隔板抽掉，让左侧气体自由膨胀到右侧直至平衡

A．气体对外做功，内能减少，温度降低

B．气体对外做功，内能不变，温度不变

C．气体不做功，内能不变，温度不变，压强减小

D．气体不做功，内能减少，压强减小

点评：学生容易出现的错误：认为气体体积变大就对外做功；认为压强减小，温度降低

5．热力学第一定律在气体中的应用

对一定质量的理想气体(除碰撞外忽略分子间的相互作用力，因此没有分子势能)，热力学第一定律ΔU=Q+W中：⑴ΔU仅由温度决定，升温时为正，降温时为负；⑵W仅由体积决定，压缩时为正，膨胀时为负；⑶Q由ΔU和W共同决定；⑷在绝热情况下Q=0，因此有ΔU= W。

[例16] 钢瓶内装有高压氧气。打开阀门氧气迅速从瓶口喷出，当内外气压相等时立即关闭阀门。过一段时间后再打开阀门，会不会再有氧气逸出？

解析：第一次打开阀门氧气“迅速”喷出，是一个绝热过程Q=0，同时氧气体积膨胀对外做功W<0，由热力学第一定律ΔU<0，即关闭阀门时瓶内氧气温度必然低于外界温度，而压强等于外界大气压；“过一段时间”经过热交换，钢瓶内氧气的温度又和外界温度相同了，由于体积未变，所以瓶内氧气压强将增大，即大于大气压，因此再次打开阀门，将会有氧气逸出。

4．气体压强的计算

气体压强的确定要根据气体所处的外部条件，往往需要利用跟气体接触的液柱和活塞等物体的受力情况和运动情况计算。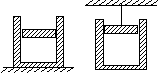

[例8] 竖直平面内有右图所示的均匀玻璃管，内用两段水银柱封闭两段空气柱a、b，各段水银柱高度如图所示。大气压为p₀，求空气柱a、b的压强各多大？

解析：从开口端开始计算：右端为大气压p₀，同种液体同一水平面上的压强相同，所以b气柱的压强为p_b= p₀+ρg(h₂-h₁)，而a气柱的压强为p_a= p_b-ρgh₃= p₀+ρg(h₂-h₁-h₃)。

此类题求气体压强的原则就是从开口端算起(一般为大气压)，沿着液柱在竖直方向上，向下加ρgh，向上减ρgh即可(h为高度差)。

[例9] 右图中两个气缸的质量均为M，内部横截面积均为S，两个活塞的质量均为m，左边的气缸静止在水平面上，右边的活塞和气缸竖直悬挂在天花板下。两个气缸内分别封闭有一定质量的空气A、B，大气压为p₀，求封闭气体A、B的压强各多大？

　解析：求气体压强要以跟气体接触的物体为对象进行受力分析，在本题中，可取的研究对象有活塞和气缸。两种情况下活塞和气缸的受力情况的复杂程度是不同的：第一种情况下，活塞受重力、大气压力和封闭气体压力三个力作用，而且只有气体压力是未知的；气缸受重力、大气压力、封闭气体压力和地面支持力四个力，地面支持力和气体压力都是未知的，要求地面压力还得以整体为对象才能得出。因此应选活塞为对象求p_A。同理第二种情况下应以气缸为对象求p_B。得出的结论是：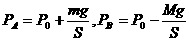

[例10]右图中气缸静止在水平面上，缸内用活塞封闭一定质量的空气。活塞的的质量为m，横截面积为S，下表面与水平方向成θ角，若大气压为p₀，求封闭气体的压强p

解析：以活塞为对象进行受力分析，关键是气体对活塞的压力方向应该垂直与活塞下表面而向斜上方，与竖直方向成θ角，接触面积也不是S而是S₁=S/cosθ。因此竖直方向受力平衡方程为：pS₁cosθ=mg+p₀S，得p=p₀+mg/S。结论跟θ角的大小无关。

[例11] 如图所示，大小不同的两个气缸A、B固定在水平面上，缸内的横截面积分别为S_A和S_B且S_A=3S_B。两缸内各有一个活塞，在两个气缸内分别封闭一定质量的空气，并用水平杆相连。已知大气压为p₀，气缸A内空气的压强为p_A=1.2 p₀，不计活塞和气缸间的摩擦阻力，求气缸B内空气的压强p_B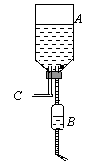

解：应该以整体为研究对象用水平方向的合力为零列方程，而不能认为A、B内气体的压强相等。因为两个活塞的横截面积是不同的。应该以两个活塞和连杆整体为研究对象进行受力分析，同时要考虑大气压的影响，受力图如上。在水平方向上有：p_AS_A+p₀S_B=p_BS_B+p₀S_A，代入S_A=3 S_B可得p_B=3p_A-2p₀=1.6p₀

本题还可以把该装置竖立起来，那么在以活塞和连杆为对象受力分析时，还应考虑到重力的作用。

[例12] 如图为医院为病人输液的部分装置，图中A为输液瓶，B为滴壶，C为进气管，与大气相通。则在输液过程中(瓶A中尚有液体)，下列说法正确的是：①瓶A中上方气体的压强随液面的下降而增大；②瓶A中液面下降，但A中上方气体的压强不变；③滴壶B中的气体压强随A中液面的下降而减小；④在瓶中药液输完以前，滴壶B中的气体压强保持不变　

A.①③　　 　　　　B.①④　　　 　　C.②③　　 　　　　D.②④

解析：进气管C端的压强始终是大气压p₀，设输液瓶A内的压强为p_A，可以得到p_A= p₀-ρgh，因此p_A将随着h的减小而增大。滴壶B的上液面与进气管C端的高度差不受输液瓶A内液面变化的影响，因此压强不便。选B。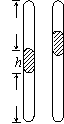

[例13] 长直均匀玻璃管内用水银柱封闭一定质量的空气后倒插入水银槽内。静止时露出水银槽面的水银柱高为h，保持温度不变，稍向上提玻璃管(管口仍在槽内水银面下)，封闭在管内的空气的体积V和压强p以及水银柱高h各如何变化？

解析：一定质量的气体在温度不变使，气体的压强p和体积V必然同时变化，而达到平衡后，p+ρgh= p₀的关系应该依然成立。假设V不变，那么p也不变，而提升后h变大，p+ρgh将大于p₀，因此管内水银柱将要下降，即封闭空气的体积V必然增大，压强p必然减小，又由于最终应该有p+ρgh= p₀，所以h必然增大。

本题也可以假设提升后p不变，进行推导，结论是完全一致的。

注意前提：管内必须封闭有一定质量的空气。若水银柱上端是真空，那h就始终满足p₀=ρgh，向上提升玻璃管不会影响h的大小，那么V就一定增大了。　　　　

[例14] 两端封闭的均匀直玻璃管竖直放置，内用高h的汞柱把管内空气分为上下两部分，静止时两段空气柱的长均为L，上端空气柱压强为p₁=2ρgh(ρ为水银的密度)。当玻璃管随升降机一起在竖直方向上做匀变速运动时，稳定后发现上端空气柱长减为2L/3。则下列说法中正确的是

A．稳定后上段空气柱的压强大于2ρgh

B．稳定后下段空气柱的压强小于3ρgh

C．升降机一定在加速上升

D．升降机可能在匀减速上升

解析：系统静止时下段空气柱的压强是3ρgh。做匀变速运动稳定后上段空气柱体积减小说明其压强增大，而下段空气柱体积增大，说明其压强减小。由水银柱的受力分析可知，其合力方向向下，因此加速度向下，可能匀加速下降，也可能匀减速上升。选ABD

[例15] 在一个固定容积的密闭容器中，加入3L的X(g)和2L的Y(g)，在一定条件下这两种气体发生反应而生成另两种气体：4X(g)+3Y(g)　 2Q(g)+nR(g)，达到平衡后，容器内温度不变，而混合气体的压强比原来增大，则该反应方程中的n值可能为

　A．3　　　 B．4　　　 C．5　　　　 D．6 　　　

解析：由于反应前后所有物质都是气态，设反应前后的总的物质的量分别为N₁、N₂，由于在一定温度和体积下，气体的压强和气体物质的量成正比，因此生成物的物质的量应该大于反应前的物质的量，只能取n=6，选D。

3．气体的体积、压强、温度间的关系(新大纲只要求定性介绍)

(1)一定质量的气体，在温度不变的情况下，体积减小时，压强增大，体积增大时，压强减小。

(2)一定质量的气体，在压强不变的情况下，温度升高，体积增大。

(3)一定质量的气体，在体积不变的情况下，温度升高，压强增大。

2．气体分子动理论

(1)气体分子运动的特点是：①气体分子间的距离大约是分子直径的10倍，分子间的作用力十分微弱。通常认为，气体分子除了相互碰撞或碰撞器壁外，不受力的作用。②每个气体分子的运动是杂乱无章的，但对大量分子的整体来说，分子的运动是有规律的。研究的方法是统计方法。气体分子的速率分布规律遵从统计规律。在一定温度下，某种气体的分子速率分布是确定的，可以求出这个温度下该种气体分子的平均速率。

(2)用分子动理论解释气体压强的产生(气体压强的微观意义)。气体的压强是大量分子频繁碰撞器壁产生的。压强的大小跟两个因素有关：①气体分子的平均动能，②分子的密集程度。

1．气体的状态参量

(1)温度：温度在宏观上表示物体的冷热程度；在微观上是分子平均动能的标志。

热力学温度是国际单位制中的基本量之一，符号T，单位K(开尔文)；摄氏温度是导出单位，符号t，单位℃(摄氏度)。关系是t=T-T₀，其中T₀=273.15K，摄氏度不再采用过去的定义。

两种温度间的关系可以表示为：T = t+273.15K和ΔT =Δt，要注意两种单位制下每一度的间隔是相同的。

0K是低温的极限，它表示所有分子都停止了热运动。可以无限接近，但永远不能达到。

(2)体积。气体总是充满它所在的容器，所以气体的体积总是等于盛装气体的容器的容积。

(3)压强。气体的压强是由于气体分子频繁碰撞器壁而产生的。(绝不能用气体分子间的斥力解释！)

一般情况下不考虑气体本身的重量，所以同一容器内气体的压强处处相等。但大气压在宏观上可以看成是大气受地球吸引而产生的重力而引起的。(例如在估算地球大气的总重量时可以用标准大气压乘以地球表面积。)

压强的国际单位是帕，符号Pa，常用的单位还有标准大气压(atm)和毫米汞柱(mmHg)。它们间的关系是：1 atm=1.013×10⁵Pa=760 mmHg； 1 mmHg=133.3Pa。

7．热力学第二定律

(1)热传导的方向性。热传导的过程是有方向性的，这个过程可以向一个方向自发地进行(热量会自发地从高温物体传给低温物体)，但是向相反的方向却不能自发地进行。

(2)第二类永动机不可能制成。我们把没有冷凝器，只有单一热源，从单一热源吸收热量全部用来做功，而不引起其它变化的热机称为第二类永动机。这表明机械能和内能的转化过程具有方向性：机械能可以全部转化成内能，内能却不能全部转化成机械能。

(3)热力学第二定律。表述：①不可能使热量由低温物体传递到高温物体，而不引起其他变化(按热传导的方向性表述)。②不可能从单一热源吸收热量并把它全部用来做功，而不引起其他变化(按机械能和内能转化过程的方向性表述)。③第二类永动机是不可能制成的。

热力学第二定律使人们认识到：自然界种进行的涉及热现象的宏观过程都具有方向性。它揭示了有大量分子参与的宏观过程的方向性，使得它成为独立于热力学第一定律的一个重要的自然规律。

(4)能量耗散。自然界的能量是守恒的，但是有的能量便于利用，有些能量不便于利用。很多事例证明，我们无法把流散的内能重新收集起来加以利用。这种现象叫做能量的耗散。它从能量转化的角度反映出自然界中的宏观现象具有方向性。

[例7](2004年高考科研测试)图中气缸内盛有定量的理想气体，气缸壁是导热的，缸外环境保持恒温，活塞与气缸壁的接触是光滑的，但不漏气。现将活塞杆与外界连接使其缓慢的向右移动，这样气体将等温膨胀并通过杆对外做功。若已知理想气体的内能只与温度有关，则下列说法正确的是

A．气体是从单一热源吸热，全用来对外做功，因此此过程违反热力学第二定律

B．气体是从单一热源吸热，但并未全用来对外做功，所以此过程不违反热力学第二定律

C．气体是从单一热源吸热，全用来对外做功，但此过程不违反热力学第二定律

D．ABC三种说法都不对

答案：C

6．能量守恒定律

能量守恒定律指出：能量即不会凭空产生，也不会凭空消失，它只能从一种形式转化为别的形式，或者从一个物体转移到别的物体，在转化或转移的过程中其总量不变。

能量守恒定律是自然界普遍适用的规律之一，是研究自然科学的强有力的武器之一。

[例6] “奋进号”航天飞机进行过一次太空飞行，其主要任务是给国际空间站安装太阳能电池板。该太阳能电池板长L=73m，宽d=12m，将太阳能转化为电能的转化率为η=20%，已知太阳的辐射总功率为P₀=3.83×10²⁶W，地日距离为R₀=1.5×10¹¹m，国际空间站离地面的高度为h=370km，它绕地球做匀速圆周运动约有一半时间在地球的阴影内，所以在它能发电的时间内将把所发电的一部分储存在蓄电池内。由以上数据，估算这个太阳能电池板能对国际空间站提供的平均功率是多少？

解析：由于国际空间站离地面的高度仅为地球半径的约二十分之一，可认为是近地卫星，h远小于R₀，因此它离太阳的距离可认为基本不变，就是地日距离R₀。太阳的辐射功率应视为均匀分布在以太阳为圆心，地日距离为半径的球面上，由此可以算出每平方米接收到的太阳能功率I₀=P₀/4πR₀²=1.35kW/m²(该数据被称为太阳常数)，再由电池板的面积和转化率，可求出其发电时的电功率为P=I₀Ldη=2.6×10⁵W，由于每天只有一半时间可以发电，所以平均功率只是发电时电功率的一半即130kW。

5．热力学第一定律

做功和热传递都能改变物体的内能。也就是说，做功和热传递对改变物体的内能是等效的。但从能量转化和守恒的观点看又是有区别的：做功是其他能和内能之间的转化，功是内能转化的量度；而热传递是内能间的转移，热量是内能转移的量度。

外界对物体所做的功W加上物体从外界吸收的热量Q等于物体内能的增加ΔU，即ΔU=Q+W 这在物理学中叫做热力学第一定律。

在这个表达式中，当外界对物体做功时W取正，物体克服外力做功时W取负；当物体从外界吸热时Q取正，物体向外界放热时Q取负；ΔU为正表示物体内能增加，ΔU为负表示物体内能减小。

[例5] 下列说法中正确的是

A.物体吸热后温度一定升高

B.物体温度升高一定是因为吸收了热量

C.0℃的冰化为0℃的水的过程中内能不变

D.100℃的水变为100℃的水汽的过程中内能增大

解析：吸热后物体温度不一定升高，例如冰融化为水或水沸腾时都需要吸热，而温度不变，这时吸热后物体内能的增加表现为分子势能的增加，所以A不正确。做功也可以使物体温度升高，例如用力多次来回弯曲铁丝，弯曲点铁丝的温度会明显升高，这是做功增加了物体的内能，使温度上升，所以B不正确。冰化为水时要吸热，内能中的分子动能不变，但分子势能增加，因此内能增加，所以C不正确。水沸腾时要吸热，内能中的分子动能不变但分子势能增加，所以内能增大，D正确。