0 138648 138656 138662 138666 138672 138674 138678 138684 138686 138692 138698 138702 138704 138708 138714 138716 138722 138726 138728 138732 138734 138738 138740 138742 138743 138744 138746 138747 138748 138750 138752 138756 138758 138762 138764 138768 138774 138776 138782 138786 138788 138792 138798 138804 138806 138812 138816 138818 138824 138828 138834 138842 447348
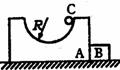 [例1]如图所示,A和B并排放在光滑的水平面上,A上有一光滑的半径为R的半圆轨道,半圆轨道右侧顶点有一小物体C,C由顶点自由滑下,设A、B、C的质量均为m.求:
[例1]如图所示,A和B并排放在光滑的水平面上,A上有一光滑的半径为R的半圆轨道,半圆轨道右侧顶点有一小物体C,C由顶点自由滑下,设A、B、C的质量均为m.求: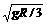 ,vC=-2
,vC=-2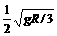 .
.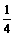 mgR.
mgR.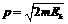 ,常用于比较动能相同而质量不同物体的动量大小;
,常用于比较动能相同而质量不同物体的动量大小;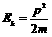 常用来比较动量相同而质量不同物体的动能大小.
常用来比较动量相同而质量不同物体的动能大小.