0 138628 138636 138642 138646 138652 138654 138658 138664 138666 138672 138678 138682 138684 138688 138694 138696 138702 138706 138708 138712 138714 138718 138720 138722 138723 138724 138726 138727 138728 138730 138732 138736 138738 138742 138744 138748 138754 138756 138762 138766 138768 138772 138778 138784 138786 138792 138796 138798 138804 138808 138814 138822 447348
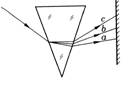 如图所示,一细光束通过玻璃三棱镜折射后分成a、b、c三束单色光,则这三种单色光( )
如图所示,一细光束通过玻璃三棱镜折射后分成a、b、c三束单色光,则这三种单色光( )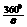 不是整数时,成像个数为
不是整数时,成像个数为 个;
个;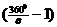 个. 以上仅限于一般情况,特殊情况需作图讨论.
个. 以上仅限于一般情况,特殊情况需作图讨论.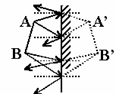 B、对称法:先根据平面镜成像有对称性的特点,确定像点的位置,再补画入射光线和反射光线.注意实际光线用实线且标前头,镜后的反向延长线用虚线,不标箭头.
B、对称法:先根据平面镜成像有对称性的特点,确定像点的位置,再补画入射光线和反射光线.注意实际光线用实线且标前头,镜后的反向延长线用虚线,不标箭头.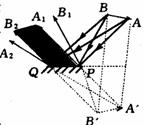 [例5]如图所示,AB沿平面镜所成的像,能观察到全像的区域.
[例5]如图所示,AB沿平面镜所成的像,能观察到全像的区域.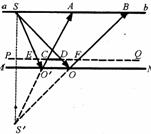 [例6]有-竖直放置的平面镜M,居平面镜前45cm处有一与平面镜平行放置的平板ab,ab靠镜一侧有一点光源S,现要在离平面镜 5cm的PQ虚线上的某一处放一平行于平面镜的挡板,使反射光不能照射到ab板上的A B部分.已知:SA=45cm,AB=45cm.求挡光板的最小宽度是多少?
[例6]有-竖直放置的平面镜M,居平面镜前45cm处有一与平面镜平行放置的平板ab,ab靠镜一侧有一点光源S,现要在离平面镜 5cm的PQ虚线上的某一处放一平行于平面镜的挡板,使反射光不能照射到ab板上的A B部分.已知:SA=45cm,AB=45cm.求挡光板的最小宽度是多少?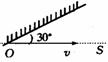 解析:利用物像对称性作出开始时光源S的像S/.设在t时间里平面镜沿水平OS方向平移到S(即镜面与光源S重合),则此时像与物重合,又由物像与镜面对称知:此过程像S/的运动方向必沿着S/S方向(垂直于镜面).
解析:利用物像对称性作出开始时光源S的像S/.设在t时间里平面镜沿水平OS方向平移到S(即镜面与光源S重合),则此时像与物重合,又由物像与镜面对称知:此过程像S/的运动方向必沿着S/S方向(垂直于镜面).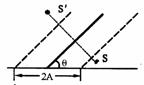 [例9]如图所示,S为静止的点光源,M为与水平成θ角的平面镜,若平面镜沿水平方向做振幅为A的简谐运动,则光源在平面镜中所成的虚像S/的运动是( )
[例9]如图所示,S为静止的点光源,M为与水平成θ角的平面镜,若平面镜沿水平方向做振幅为A的简谐运动,则光源在平面镜中所成的虚像S/的运动是( )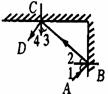 [例4]如图所示,两个镜相成直角,入射光线AB经过两次反射后的光线为CD.今以两镜的交线为轴,将镜转动100,两平面镜仍保持垂直,在入射光线AB保持不变的情况下,经过两次反射后,反射光线为C/D/,则C/D/与CD的位置关系为( A )
[例4]如图所示,两个镜相成直角,入射光线AB经过两次反射后的光线为CD.今以两镜的交线为轴,将镜转动100,两平面镜仍保持垂直,在入射光线AB保持不变的情况下,经过两次反射后,反射光线为C/D/,则C/D/与CD的位置关系为( A )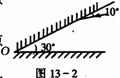 则: (D)
则: (D) [例6]如图所示,在A点有一个小球,紧靠小球的左方有一个点光源S。现将小球从A点正对着竖直墙平抛出去,打到竖直墙之前,小球在点光源照射下的影子在墙上的运动是
[例6]如图所示,在A点有一个小球,紧靠小球的左方有一个点光源S。现将小球从A点正对着竖直墙平抛出去,打到竖直墙之前,小球在点光源照射下的影子在墙上的运动是 ,因此影子在墙上的运动是匀速运动。
,因此影子在墙上的运动是匀速运动。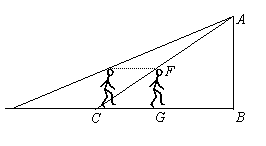 [例7]某人身高1.8 m,沿一直线以2 m/s的速度前进,其正前方离地面5 m高处有一盏路灯,试求人的影子在水平地面上的移动速度。
[例7]某人身高1.8 m,沿一直线以2 m/s的速度前进,其正前方离地面5 m高处有一盏路灯,试求人的影子在水平地面上的移动速度。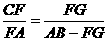
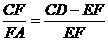
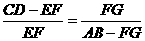 即
即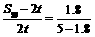 解得S影=3.125t 。
解得S影=3.125t 。 反射定律:反射光线跟入射光线和法线在同一平面内,且反射光线和人射光线分居法线两侧,反射角等于入射角.
反射定律:反射光线跟入射光线和法线在同一平面内,且反射光线和人射光线分居法线两侧,反射角等于入射角.