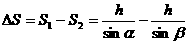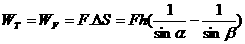0 137493 137501 137507 137511 137517 137519 137523 137529 137531 137537 137543 137547 137549 137553 137559 137561 137567 137571 137573 137577 137579 137583 137585 137587 137588 137589 137591 137592 137593 137595 137597 137601 137603 137607 137609 137613 137619 137621 137627 137631 137633 137637 137643 137649 137651 137657 137661 137663 137669 137673 137679 137687 447348
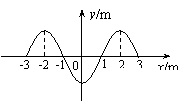 ②质点振动周期的最大值为0.4s
②质点振动周期的最大值为0.4s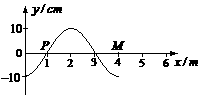 四川省内江市2010届高三二模模拟如图所示,一列简谐横波沿x轴正向传播,从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷。下列说法中正确的是 ( A )
四川省内江市2010届高三二模模拟如图所示,一列简谐横波沿x轴正向传播,从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷。下列说法中正确的是 ( A )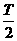 的整数倍
的整数倍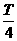 ,则t和(t+△t)两时刻,振子的位移大小之和一定等于振幅
,则t和(t+△t)两时刻,振子的位移大小之和一定等于振幅 )时刻振子速度的大小一定相等
)时刻振子速度的大小一定相等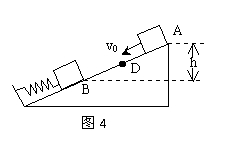 例5、如图4所示,质量m=2kg的物体,从光滑斜面的顶端A点以V0=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。
例5、如图4所示,质量m=2kg的物体,从光滑斜面的顶端A点以V0=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。 6、用功能原理求变力做功
6、用功能原理求变力做功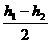 以上部分的水等效地移至右管,如图6中的斜线所示。最后用功能关系,重力所做的功等于重力势能的减少量,选用AB所在的平面为零重力势能平面,则画斜线部分从左管移之右管所减少的重力势能为:
以上部分的水等效地移至右管,如图6中的斜线所示。最后用功能关系,重力所做的功等于重力势能的减少量,选用AB所在的平面为零重力势能平面,则画斜线部分从左管移之右管所减少的重力势能为: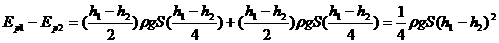
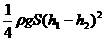 .
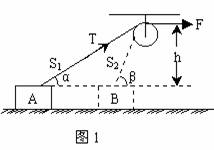
.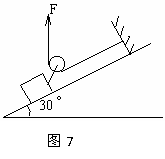 当牵引动滑轮两根细绳不平行时,但都是恒力,此时若将此二力合成为一个恒力再计算这个恒力的功,则计算过程较复杂。但若等效为两个恒力功的代数和,将使计算过程变得非常简便。
当牵引动滑轮两根细绳不平行时,但都是恒力,此时若将此二力合成为一个恒力再计算这个恒力的功,则计算过程较复杂。但若等效为两个恒力功的代数和,将使计算过程变得非常简便。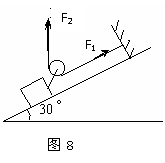 J B.150J
J B.150J )
)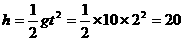 m,
m,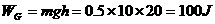 ,平均功率
,平均功率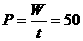 W。
W。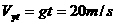 ,所以t=2s末瞬时功率
,所以t=2s末瞬时功率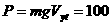 W。
W。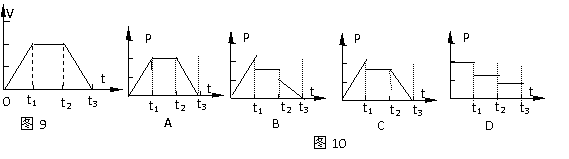 例9、起重机的钢索将重物由地面吊到空中某个高度,其速度图象如图9所示,则钢索拉力的功率随时间变化的图象可能是图10中的哪一个?
例9、起重机的钢索将重物由地面吊到空中某个高度,其速度图象如图9所示,则钢索拉力的功率随时间变化的图象可能是图10中的哪一个?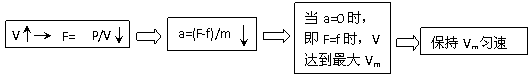
 =12 m/s
=12 m/s

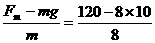 m/s2=5 m/s2,末速度Vt=
m/s2=5 m/s2,末速度Vt=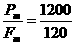 =10 m/s
=10 m/s 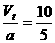 s=2 s,上升高度为h=
s=2 s,上升高度为h=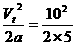 =10 m
=10 m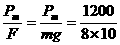 =15 m/s
=15 m/s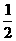 mV2m-
mV2m-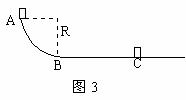
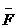 所做的功。由题意可知f0=0.05×105×10N=5×104N,所以前进100m过程中的平均牵引力:
所做的功。由题意可知f0=0.05×105×10N=5×104N,所以前进100m过程中的平均牵引力: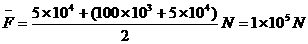
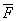 S=1×105×100J=1×107J。
S=1×105×100J=1×107J。