0 137582 137590 137596 137600 137606 137608 137612 137618 137620 137626 137632 137636 137638 137642 137648 137650 137656 137660 137662 137666 137668 137672 137674 137676 137677 137678 137680 137681 137682 137684 137686 137690 137692 137696 137698 137702 137708 137710 137716 137720 137722 137726 137732 137738 137740 137746 137750 137752 137758 137762 137768 137776 447348
 v1=v0-aAt1
v1=v0-aAt1
 (13分)如图甲所示,固定的光滑水平绝缘轨道与竖直放置的光滑绝缘的圆形轨道平滑连接,圆形轨道处于水平向右的匀强电场中,圆形轨道的最低点有A、B、C、D四个小球.已知mA=mB=mC=mD=0.3 kg,A球带正电,电荷量为q,其余小球均不带电.电场强度E=,圆形轨道半径R=0.2 m,小球C、D与处于原长的轻弹簧2连接,小球A、B中间压缩一轻且短的弹簧1,轻弹簧与A、B均不连接,由静止释放A、B后,A恰能做完整的圆周运动.B被弹开后与C小球碰撞且粘连在一起,设碰撞时间极短.g取10
m/s2,求:
(13分)如图甲所示,固定的光滑水平绝缘轨道与竖直放置的光滑绝缘的圆形轨道平滑连接,圆形轨道处于水平向右的匀强电场中,圆形轨道的最低点有A、B、C、D四个小球.已知mA=mB=mC=mD=0.3 kg,A球带正电,电荷量为q,其余小球均不带电.电场强度E=,圆形轨道半径R=0.2 m,小球C、D与处于原长的轻弹簧2连接,小球A、B中间压缩一轻且短的弹簧1,轻弹簧与A、B均不连接,由静止释放A、B后,A恰能做完整的圆周运动.B被弹开后与C小球碰撞且粘连在一起,设碰撞时间极短.g取10
m/s2,求: (1)因qE=mg,由题意知小球恰好能通过图乙中的P点,设经过P点的速度为v,由小球A的重力和电场力的合力提供向心力有:
(1)因qE=mg,由题意知小球恰好能通过图乙中的P点,设经过P点的速度为v,由小球A的重力和电场力的合力提供向心力有: mv0=m+Mv
mv0=m+Mv 如图所示,在光滑的水平轨道上有甲、乙两个等大的小球沿轨道向右运动,取向右为正方向,它们的动量分别为p1=5 kg·m/s 和
p2=7 kg·m/s.若两球能发生正碰,则碰后两球动量的增量Δp1和Δp2可能是( )
如图所示,在光滑的水平轨道上有甲、乙两个等大的小球沿轨道向右运动,取向右为正方向,它们的动量分别为p1=5 kg·m/s 和
p2=7 kg·m/s.若两球能发生正碰,则碰后两球动量的增量Δp1和Δp2可能是( )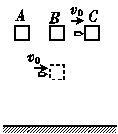 当动量做选项D所述的变化时,系统的动能增大,故不可能成立.
当动量做选项D所述的变化时,系统的动能增大,故不可能成立. 如图所示,一沙袋用无弹性轻绳悬于O点.开始时沙袋处于静止,此后用弹丸以水平速度击中沙袋后均未穿出.第一次弹丸的速度为v1,打入沙袋后二者共同摆动的最大摆角为30°;当其第一次返回图示位置时,第二粒弹丸以水平速度v2又击中沙袋,使沙袋向右摆动且最大摆角仍为30°.若弹丸的质量是沙袋质量的,则以下结论中正确的是( )
如图所示,一沙袋用无弹性轻绳悬于O点.开始时沙袋处于静止,此后用弹丸以水平速度击中沙袋后均未穿出.第一次弹丸的速度为v1,打入沙袋后二者共同摆动的最大摆角为30°;当其第一次返回图示位置时,第二粒弹丸以水平速度v2又击中沙袋,使沙袋向右摆动且最大摆角仍为30°.若弹丸的质量是沙袋质量的,则以下结论中正确的是( ) 如图所示,静止在水平面上内壁光滑的盒子中有一小球,盒子与小球的质量均为m,盒子与水平面间的动摩擦因数为μ.现给盒子一个水平向右的冲量I,设盒子与小球发生多次没有机械能损失的碰撞,最终都停下来.用t表示从瞬时冲量作用在盒子上到最终停下来所用的时间,s表示以上过程中盒子的位移.则下列各式正确的是( )
如图所示,静止在水平面上内壁光滑的盒子中有一小球,盒子与小球的质量均为m,盒子与水平面间的动摩擦因数为μ.现给盒子一个水平向右的冲量I,设盒子与小球发生多次没有机械能损失的碰撞,最终都停下来.用t表示从瞬时冲量作用在盒子上到最终停下来所用的时间,s表示以上过程中盒子的位移.则下列各式正确的是( )