0 137566 137574 137580 137584 137590 137592 137596 137602 137604 137610 137616 137620 137622 137626 137632 137634 137640 137644 137646 137650 137652 137656 137658 137660 137661 137662 137664 137665 137666 137668 137670 137674 137676 137680 137682 137686 137692 137694 137700 137704 137706 137710 137716 137722 137724 137730 137734 137736 137742 137746 137752 137760 447348
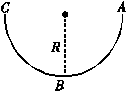 (14分)如图甲所示,竖直平面上有一光滑绝缘的半圆形轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R . 一个质量为m的带正电的小球从槽右端的A处无初速度地沿轨道下滑,滑到最低点B时对槽底压力为2mg.
求小球在滑动过程中的最大速度.
(14分)如图甲所示,竖直平面上有一光滑绝缘的半圆形轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R . 一个质量为m的带正电的小球从槽右端的A处无初速度地沿轨道下滑,滑到最低点B时对槽底压力为2mg.
求小球在滑动过程中的最大速度.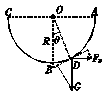 得WE=-mgR
得WE=-mgR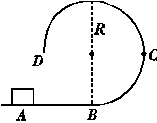 (13分)如图甲所示,光滑绝缘的水平轨道AB与半径为R的光滑绝缘圆形轨道BCD平滑连接,圆形轨道竖直放置,空间存在水平向右的匀强电场,场强为E.今有一质量为m、电荷量为q的滑块,其所受的电场力大小等于重力.滑块在A点由静止释放,若它能沿圆轨道运动到与圆心等高的D点,则AB至少为多长?
(13分)如图甲所示,光滑绝缘的水平轨道AB与半径为R的光滑绝缘圆形轨道BCD平滑连接,圆形轨道竖直放置,空间存在水平向右的匀强电场,场强为E.今有一质量为m、电荷量为q的滑块,其所受的电场力大小等于重力.滑块在A点由静止释放,若它能沿圆轨道运动到与圆心等高的D点,则AB至少为多长?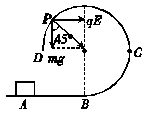 故在P点,有:
故在P点,有: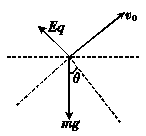 解析:
解析: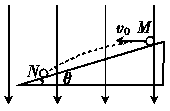 解析:由题意知,小球的电场力可以向下,也可以向上,向上时的大小小于mg,
解析:由题意知,小球的电场力可以向下,也可以向上,向上时的大小小于mg,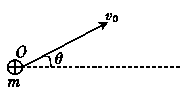 故可得W总=mv2-mv,选项C正确.
故可得W总=mv2-mv,选项C正确.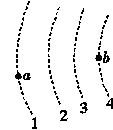 图中虚线为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为零.一带正电的点电荷只在静电力的作用下运动,经过a、b点时的动能分别为26 eV和5
eV.当这一点电荷运动到某一位置.其电势能变为-8 eV时, 它的动能为( )
图中虚线为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为零.一带正电的点电荷只在静电力的作用下运动,经过a、b点时的动能分别为26 eV和5
eV.当这一点电荷运动到某一位置.其电势能变为-8 eV时, 它的动能为( )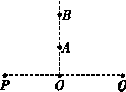 如图所示,两个等量的正点电荷Q、P,连线中点为O,在中垂线上有A、B两点,已知OA<OB,A、B两点的电场强度及电势分别为EA、EB、φA、φB,则( )
如图所示,两个等量的正点电荷Q、P,连线中点为O,在中垂线上有A、B两点,已知OA<OB,A、B两点的电场强度及电势分别为EA、EB、φA、φB,则( )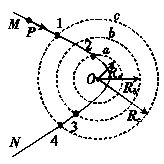 如图所示,O是一固定的点电荷,另一点电荷P从很远处以初速度v0射入点电荷O的电场,在电场力作用下的运动轨迹是曲线MN.a、b、c是以O为圆心,Ra、Rb、Rc为半径画出的三个圆.Rc=3Ra,Rb=2Ra.1、2、3、4为轨迹MN与三个圆的一些交点,以|W12|
表示点电荷P由1到2的过程中电场力做的功的大小,|W34|表示点电荷P由3到4的过程中电场力做的功的大小,则( )
如图所示,O是一固定的点电荷,另一点电荷P从很远处以初速度v0射入点电荷O的电场,在电场力作用下的运动轨迹是曲线MN.a、b、c是以O为圆心,Ra、Rb、Rc为半径画出的三个圆.Rc=3Ra,Rb=2Ra.1、2、3、4为轨迹MN与三个圆的一些交点,以|W12|
表示点电荷P由1到2的过程中电场力做的功的大小,|W34|表示点电荷P由3到4的过程中电场力做的功的大小,则( )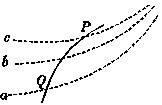 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力的作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )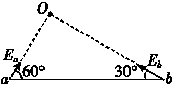 如图所示,真空中O点处有一点电荷,在它产生的电场中有a、b两点,a点的场强大小为Ea,方向与ab连线成60°角;b点的场强大小为Eb,方向与a、b连线成30°角,则关于a、b两点场强大小及电势φa、φb的高低关系正确的是( )
如图所示,真空中O点处有一点电荷,在它产生的电场中有a、b两点,a点的场强大小为Ea,方向与ab连线成60°角;b点的场强大小为Eb,方向与a、b连线成30°角,则关于a、b两点场强大小及电势φa、φb的高低关系正确的是( )