0 136998 137006 137012 137016 137022 137024 137028 137034 137036 137042 137048 137052 137054 137058 137064 137066 137072 137076 137078 137082 137084 137088 137090 137092 137093 137094 137096 137097 137098 137100 137102 137106 137108 137112 137114 137118 137124 137126 137132 137136 137138 137142 137148 137154 137156 137162 137166 137168 137174 137178 137184 137192 447348
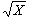 kgm/s,小车质量M=3.6kg,不计能量损失。求:
kgm/s,小车质量M=3.6kg,不计能量损失。求:
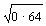 =3.2m/s
=3.2m/s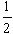 mVB2
mVB2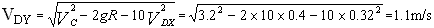
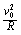 [1]
[1]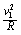 [3]
[3] 
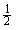 m2V12+m2g2R=
m2V12+m2g2R=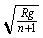 =
=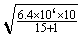 =2.0X103 m/s
=2.0X103 m/s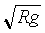 =7.9X103m/s,这就是第一宇宙速度,即环绕速度。
=7.9X103m/s,这就是第一宇宙速度,即环绕速度。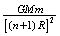 =
=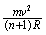 [1]
[1] 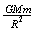 [2]
[2]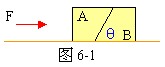
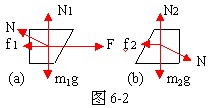
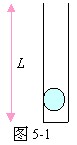
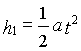
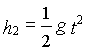
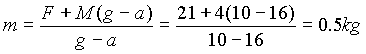
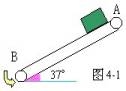
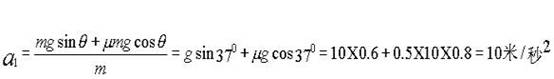
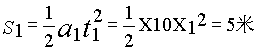
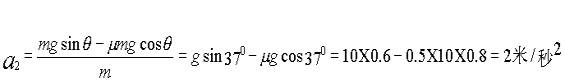
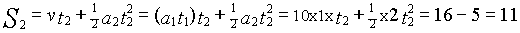
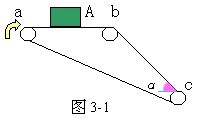
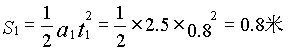
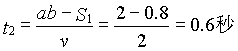
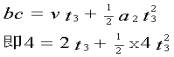
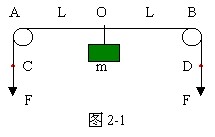
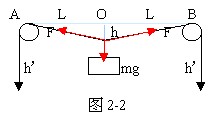
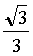 L
[1]
L
[1]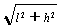 -L [2]
-L [2]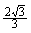 -1)mgL
-1)mgL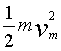 [4]
[4]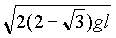
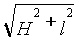 -L,联立解得:H=
-L,联立解得:H=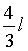 。
。
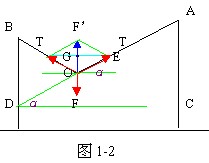
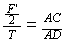 得:
得: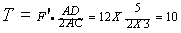 牛。
牛。