0 136778 136786 136792 136796 136802 136804 136808 136814 136816 136822 136828 136832 136834 136838 136844 136846 136852 136856 136858 136862 136864 136868 136870 136872 136873 136874 136876 136877 136878 136880 136882 136886 136888 136892 136894 136898 136904 136906 136912 136916 136918 136922 136928 136934 136936 136942 136946 136948 136954 136958 136964 136972 447348
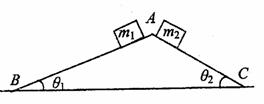
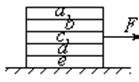 (2009 届江苏苏州中学高三月考) 五本书相叠放在水平桌面上,用水平力F拉中间的书C但未拉动,各书仍静止(如图)。关于它们所受摩擦力的情况,以下判断中正确的是 ( ABD )
(2009 届江苏苏州中学高三月考) 五本书相叠放在水平桌面上,用水平力F拉中间的书C但未拉动,各书仍静止(如图)。关于它们所受摩擦力的情况,以下判断中正确的是 ( ABD ) A.等干零
A.等干零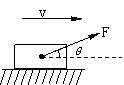 2009上海南汇区高三期末)如图所示,质量为m的物体放在水平桌面上,在与水平方向成θ角的拉力F作用下加速向前运动,已知物体与桌面间的动摩擦因数为μ,则下列判断正确的是
( B )
2009上海南汇区高三期末)如图所示,质量为m的物体放在水平桌面上,在与水平方向成θ角的拉力F作用下加速向前运动,已知物体与桌面间的动摩擦因数为μ,则下列判断正确的是
( B )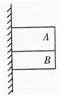 D.物体受到地面的的支持力为mg-F·sinθ
D.物体受到地面的的支持力为mg-F·sinθ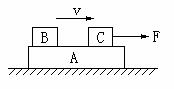 受几个力的说法正确的是 ( A )
受几个力的说法正确的是 ( A )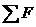 =0的平衡条件从本质上看应该是处于平衡状态下的物体所受到的各个外力之间的某种矢量关系,准确把握平衡条件所表现出的矢量关系,就能在平衡条件的应用中充分展现其应用的技巧。
=0的平衡条件从本质上看应该是处于平衡状态下的物体所受到的各个外力之间的某种矢量关系,准确把握平衡条件所表现出的矢量关系,就能在平衡条件的应用中充分展现其应用的技巧。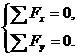
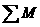 =0.
=0.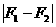 ≤F≤F1+F2.
≤F≤F1+F2.