0 136731 136739 136745 136749 136755 136757 136761 136767 136769 136775 136781 136785 136787 136791 136797 136799 136805 136809 136811 136815 136817 136821 136823 136825 136826 136827 136829 136830 136831 136833 136835 136839 136841 136845 136847 136851 136857 136859 136865 136869 136871 136875 136881 136887 136889 136895 136899 136901 136907 136911 136917 136925 447348
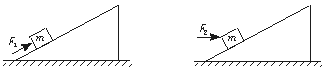
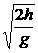 );a与b比较,两者平均速度大小相同(末动能相同);但显然a的位移大,所以用的时间长,因此A、B都不对。由于机械能守恒,c的机械能最大(有初动能),到地面时末动能也大,因此C也不对。a、b的初动量都是零,末动量大小又相同,所以动量变化大小相同;b、c所受冲量相同,所以动量变化大小也相同,故D正确。
);a与b比较,两者平均速度大小相同(末动能相同);但显然a的位移大,所以用的时间长,因此A、B都不对。由于机械能守恒,c的机械能最大(有初动能),到地面时末动能也大,因此C也不对。a、b的初动量都是零,末动量大小又相同,所以动量变化大小相同;b、c所受冲量相同,所以动量变化大小也相同,故D正确。 [例4] 海岸炮将炮弹水平射出。炮身质量(不含炮弹)为M,每颗炮弹质量为m。当炮身固定时,炮弹水平射程为s,那么当炮身不固定时,发射同样的炮弹,水平射程将是多少?
[例4] 海岸炮将炮弹水平射出。炮身质量(不含炮弹)为M,每颗炮弹质量为m。当炮身固定时,炮弹水平射程为s,那么当炮身不固定时,发射同样的炮弹,水平射程将是多少?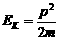 知,在动量大小相同的情况下,物体的动能和质量成反比,炮弹的动能
知,在动量大小相同的情况下,物体的动能和质量成反比,炮弹的动能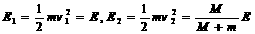 ,由于平抛射高相等,两次射程的比等于抛出时初速度之比
,由于平抛射高相等,两次射程的比等于抛出时初速度之比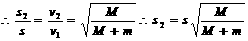
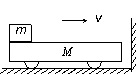 [例5] 质量M的小车左端放有质量m的铁块,以共同速度v沿光滑水平面向竖直墙运动,车与墙碰撞的时间极短,不计动能损失。动摩擦因数μ,车长L,铁块不会到达车的右端。到最终相对静止为止,摩擦生热多少?
[例5] 质量M的小车左端放有质量m的铁块,以共同速度v沿光滑水平面向竖直墙运动,车与墙碰撞的时间极短,不计动能损失。动摩擦因数μ,车长L,铁块不会到达车的右端。到最终相对静止为止,摩擦生热多少?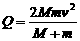 ;当M=m时,显然最终共同速度为零,当M<m时,相对静止时的共同速度必向右,再次与墙相碰,直到小车停在墙边,后两种情况的摩擦生热都等于系统的初动能
;当M=m时,显然最终共同速度为零,当M<m时,相对静止时的共同速度必向右,再次与墙相碰,直到小车停在墙边,后两种情况的摩擦生热都等于系统的初动能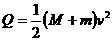
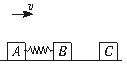 [例6]
用轻弹簧相连的质量均为2 kg的A、B两物块都以v= 6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量4 kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动.求:在以后的运动中:
[例6]
用轻弹簧相连的质量均为2 kg的A、B两物块都以v= 6 m/s的速度在光滑的水平地面上运动,弹簧处于原长,质量4 kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动.求:在以后的运动中: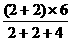 m/s=3 m/s
m/s=3 m/s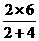 =2 m/s
=2 m/s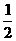 (mB+mC)
(mB+mC)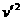 +
+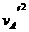
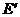 >E是不可能的
>E是不可能的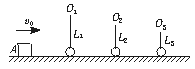
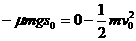 得s0=25 m
得s0=25 m 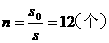
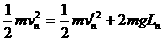 ①
①
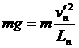 ②
②  ③
③
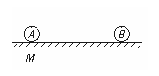 [例8] 如图所示,两个小球A和B质量分别是mA=2.0 kg,mB=1.6 kg.球A静止在光滑水平面上的M点,球B在水平面上从远处沿两球的中心连线向着球A运动.假设两球相距L≤18 m时存在着恒定的斥力F,L>18 m时无相互作用力.当两球相距最近时,它们间的距离为d=2 m,此时球B的速度是4 m/s.求:
[例8] 如图所示,两个小球A和B质量分别是mA=2.0 kg,mB=1.6 kg.球A静止在光滑水平面上的M点,球B在水平面上从远处沿两球的中心连线向着球A运动.假设两球相距L≤18 m时存在着恒定的斥力F,L>18 m时无相互作用力.当两球相距最近时,它们间的距离为d=2 m,此时球B的速度是4 m/s.求: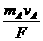
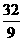 s=3.56 s
s=3.56 s 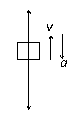

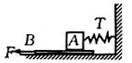 如图所示,一个本块A放在长木板B上,长木板B放在水平地面上.在恒力F作用下,长木板B以速度v匀速运动,水平弹簧秤的示数为T.下列关于摩擦力正确的是( )
如图所示,一个本块A放在长木板B上,长木板B放在水平地面上.在恒力F作用下,长木板B以速度v匀速运动,水平弹簧秤的示数为T.下列关于摩擦力正确的是( )
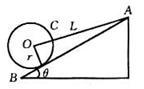
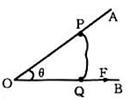 如图所示,两光滑硬杆AOB成θ角,在两杆上各套上轻环P、Q,两环用细绳相连,现用恒力F沿OB方向拉环Q ,当两环稳定时细绳拉力为( )
如图所示,两光滑硬杆AOB成θ角,在两杆上各套上轻环P、Q,两环用细绳相连,现用恒力F沿OB方向拉环Q ,当两环稳定时细绳拉力为( )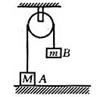 C.可以是2N,方向沿斜面向下
C.可以是2N,方向沿斜面向下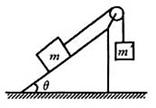 3如图所示,当倾角为45°时物体m处于静止状态,当倾角θ再增大一些,物体m仍然静止(绳子质量、滑轮摩擦不计)下列说法正确的是( )
3如图所示,当倾角为45°时物体m处于静止状态,当倾角θ再增大一些,物体m仍然静止(绳子质量、滑轮摩擦不计)下列说法正确的是( )