3、波的图像与振动图像的比较
|
|
简谐运动的振图象 |
机械波的波动图象 |
|
|
图象 |
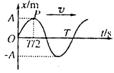 |
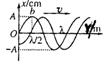 |
|
|
研究对象 |
一个振动质点 |
波传播方向所有质点 |
|
|
研究内容 |
一质点位移随时间变化规律 |
某时刻所有质点的空间分布规律 |
|
|
函数关系 |
一个质点做简谐运动时,它的位置x随时间t变化的关系 |
在某一时刻某一直线上各个质点的位置所形成的图象(横波) |
|
|
坐标 |
横轴[ |
一个质点振动的时间[ |
各质点平衡位置距坐标原点的位置(距离) |
|
纵轴 |
一个质点不同时刻相对平衡位置的位移 |
同一时刻各质点相对各自平衡位置的位移 |
|
|
形状 |
正弦函数或余弦函数的图象 |
||
|
由图象可直观得到的数据 |
周期T 振幅A |
波长λ 振幅A 波峰及波谷的位置 |
|
|
物理意义 |
表示一质点在各时刻的位移 |
表示某时刻各质点的位移 |
|
|
图象变化 |
随时间推移图象延续,但已有形态不变 |
随时间推移,图象沿传播方向平移 |
|
|
完整曲线占横坐标距离 |
表示一个周期 |
表示一个波长 |
|
|
图象上某一点的物理意义 |
在某时刻(横轴坐标)做简谐运动的物体相对平衡位置的位移(纵轴坐标) |
在某时刻,距坐标原点的距离一定(横轴坐标)的该质点的位移(纵坐标) |
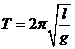 ,可知,单摆摆长不变,则周期不变,频率不变;振幅A是反映单摆运动过程中的能量大小的物理量,由
,可知,单摆摆长不变,则周期不变,频率不变;振幅A是反映单摆运动过程中的能量大小的物理量,由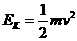 可知,摆球经过平衡位置时的动能不变,因此振幅改变,所以C正确。
可知,摆球经过平衡位置时的动能不变,因此振幅改变,所以C正确。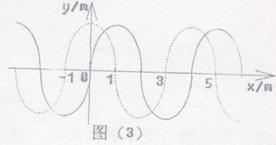
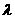 =4m。
=4m。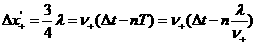 得:
得: (m/s)
(m/s)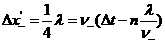 得
得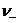 =
=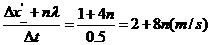
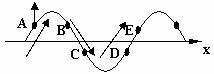
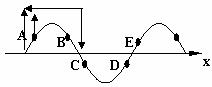
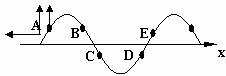
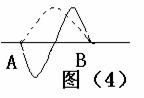 例4:一列简谐横波沿一直线由A向B传播,某一时刻A、B两点均处在平衡位置,且A、B间仅有一个波峰,B点向上振动。若经过时间t,质点B恰好在波峰位置,则该列波可能的传播速度是多少?(已知A、B相距为d)
例4:一列简谐横波沿一直线由A向B传播,某一时刻A、B两点均处在平衡位置,且A、B间仅有一个波峰,B点向上振动。若经过时间t,质点B恰好在波峰位置,则该列波可能的传播速度是多少?(已知A、B相距为d)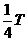 ,所以T=
,所以T=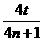 (n=0,1,2 ……)。又因为A、B间仅有一个波峰,可有图(4)中实线和虚线两种波形图。
(n=0,1,2 ……)。又因为A、B间仅有一个波峰,可有图(4)中实线和虚线两种波形图。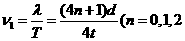 ……)
……)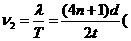 n=0,1,2……)
n=0,1,2……)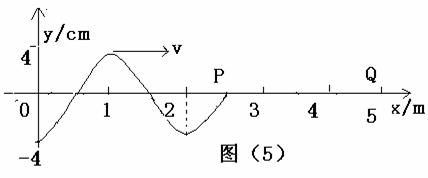 分析与解 由波形图、波的传播方向,可知P点在t=0时刻,振动方向沿-y。又因为在△t=1.1秒内P刚好第三次出现在波峰,所以2T+
分析与解 由波形图、波的传播方向,可知P点在t=0时刻,振动方向沿-y。又因为在△t=1.1秒内P刚好第三次出现在波峰,所以2T+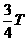 =1.1,即T=0.4S,则有
=1.1,即T=0.4S,则有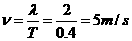 。t=0时刻波刚好传到x=2.5米的P质点处,波由P传到Q点需时间t=
。t=0时刻波刚好传到x=2.5米的P质点处,波由P传到Q点需时间t=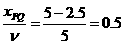 秒。因P质点开始振动方向沿-y,Q点要重复P点的振动,所以Q点刚开始振动方向也沿-y,即Q点第一次到达波峰还需3/4T,即0.3秒。综上所述Q点第一次到达波峰的时间应为0.5+0.3=0.8(秒)。
秒。因P质点开始振动方向沿-y,Q点要重复P点的振动,所以Q点刚开始振动方向也沿-y,即Q点第一次到达波峰还需3/4T,即0.3秒。综上所述Q点第一次到达波峰的时间应为0.5+0.3=0.8(秒)。 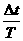 的整数部分即可。如例2中只要向右平移△x’=20×(0.5-1×0.4)=2米。若这类问题不能确定波的传播方向,则要考虑波的双向性,即有两种可能。
的整数部分即可。如例2中只要向右平移△x’=20×(0.5-1×0.4)=2米。若这类问题不能确定波的传播方向,则要考虑波的双向性,即有两种可能。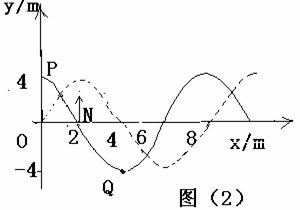
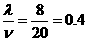 (s)
(s)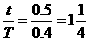 (个)
(个)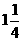 周期在波峰位置,P、Q点均在平衡位置,这样可以画出t=0. 5秒时的波形图,如图(2)虚线所示。
周期在波峰位置,P、Q点均在平衡位置,这样可以画出t=0. 5秒时的波形图,如图(2)虚线所示。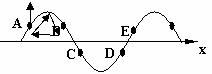
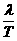 (适用于一切波)
(适用于一切波)  二、难点与突破
二、难点与突破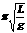 (与摆球质量,振幅无关) *弹簧振子T= 2
(与摆球质量,振幅无关) *弹簧振子T= 2 (与振子质量有关,与振幅无关)
(与振子质量有关,与振幅无关) 