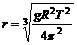3.第三宇宙速度(逃逸速度):V3=16.7km/s,使物体挣脱 引力束缚的最小发射速度。
|
[特别提醒]:第一宇宙速度是发射卫星的最小速度,却是卫星在圆周轨道上运行的最大速度。 |
[例6] 我国将要发射一颗绕月运行的探月卫星“嫦娥1号”。设该卫星的轨道是圆形的,且贴近月球表面。已知月球的质量约为地球质量的1/81,月球的半径约为地球半径的1/4,地球上的第一宇宙速度约为7.9km/s,则该探月卫星绕月运行的速率约为( )
A. 0.4 km/s B. 1.8 km/s C. 11 km/s D. 36 km/s
[解析] 设地球质量为M、半径为R,第一宇宙速度为V,月球质量为m、半径为r,第一宇宙速度为v,则根据第一宇宙速度的定义,对任一物体 ,有
,有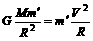 ,而
,而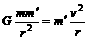 ,由两以上两式并代入数据可得
,由两以上两式并代入数据可得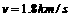
[答案] B
[规律总结] 第一宇宙速度亦即环绕速度,在高考中也频繁出现,往往是要求其它星体的第一宇宙速度,这就要求大家弄清该速度的本质意义:即卫星围绕星球表面做匀速圆周运动时的速度。
★ 高考重点热点题型探究
热点1 卫星、天体运动问题
[真题1]图7是“嫦娥一导奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
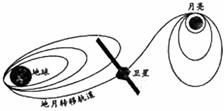 A.发射“嫦娥一号”的速度必须达到第三宇宙速度
A.发射“嫦娥一号”的速度必须达到第三宇宙速度
B.在绕月圆轨道上,卫星周期与卫星质量有关
C.卫星受月球的引力与它到月球中心距离的平方成反比
D.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
[解析] “嫦娥一号”只是摆脱地球吸引,但并未飞离太阳系,则其发射速度应大于第二宇宙速度而小于第三宇宙速度,A错。根据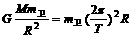 可知绕月周期与卫星质量无关,B错。根据万有引力定律可知C正确。卫星在摆脱地球引力后才能达到绕月圆轨道,故该轨道上,卫星受月球引力远大于地球引力,D错。
可知绕月周期与卫星质量无关,B错。根据万有引力定律可知C正确。卫星在摆脱地球引力后才能达到绕月圆轨道,故该轨道上,卫星受月球引力远大于地球引力,D错。
[答案] C
[名师指引] 卫星以及与航天知识相关的科技热点,在高考中频繁出现。这类问题,考查的内容相当广泛,泛及卫星运动的周期、轨道半径、发射及运动速度、发射过程中的变轨问题等。这几年航天事业在我国的高速发展,这块知识对考生的考查尤为重要。因此要求同学们对万有引力定律及相关知识全面掌握,并在平时关注相关热点问题。
[答案]⑴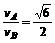 ⑵
⑵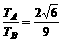 ⑶
⑶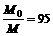
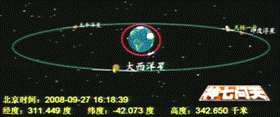 [新题导练]1. 2008年9月我国成功发射神舟七号载人航天飞船。如图所示为神舟七号绕地球飞行时的电视直播画面,图中数据显示,飞船距地面的高度约为地球半径的
[新题导练]1. 2008年9月我国成功发射神舟七号载人航天飞船。如图所示为神舟七号绕地球飞行时的电视直播画面,图中数据显示,飞船距地面的高度约为地球半径的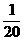 。已知地球半径为R,地面附近的重力加速度为g,设飞船、大西洋星绕地球均做匀速圆周运动。
。已知地球半径为R,地面附近的重力加速度为g,设飞船、大西洋星绕地球均做匀速圆周运动。
(1)估算神舟七号飞船在轨运行的加速度大小;
(2)已知大西洋星距地面的高度约为地球半径的6倍,估算大西洋星的速率。
热点2 黄金代换公式的应用
[真题2]宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g=10 m/s2,空气阻力不计)
⑴求该星球表面附近的重力加速度g/;⑵已知该星球的半径与地球半径之比为R星:R地=1:4,求该星球的质量与地球质量之比M星:M地。
[解析]⑴小球在地球上做竖直上抛运动,有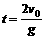 。小球在星球上做竖直上抛运动,有
。小球在星球上做竖直上抛运动,有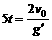 ,故
,故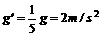 。
。
⑵地(星)球表面物体所受重力大小近似于万有引力,即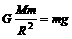 ,得
,得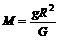 ,可解得:M星:M地=1´12:5´42=1:80
,可解得:M星:M地=1´12:5´42=1:80
[答案] 1:80
[名师指引] 星球表面的重力加速度,是联系物体运动与应用“黄金代换”公式的桥梁,因此,要重视对重力加速度的求解的应用。
[新题导练]2.我国月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大的提高了同学们对月球的关注程度。以下是某同学就有关月球的知识设计的两个问题,现请你解答:
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
(2)若某位宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t,小球落回到抛出点。已知月球半径为R月,万有引力常量为G。试求出月球的质量M月。
热点3 环绕速度(第一宇宙速度)
[真题3]我国绕月探测工程的预先研究和工程实施已取得重要进展。设地球、月球的质量分别为m1、m2,半径分别为R1、R2,人造地球卫星的第一宇宙速度为v,对应的环绕周期为T,则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为( )
A.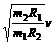 ,
,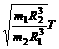 B.
B.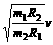 ,
, 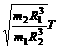
C.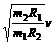 ,
,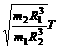 D.
D.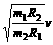 ,
, 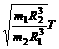
[解析] 第一宇宙速度是物体围绕星球表面作匀速圆周运动的速度,根据万有引力定律及向心力公式,质量为m绕地球表面做圆周运动的物体有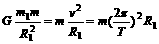 ,而质量为m绕月球表面做圆周运动的物体有
,而质量为m绕月球表面做圆周运动的物体有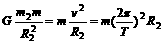 ,由以上两式相比可知A选项正确。
,由以上两式相比可知A选项正确。
[答案]A
[名师指引] 解题的关键是准确理解第一宇宙速度的意义,即物体围绕星球表面作匀速圆周运动的速度,此时物体的重力近似等于万有引力,并提供圆周运动的向心力。
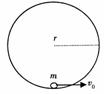 [新题导练]3.航天宇航员在月球表面完成了如下实验:如图所示,在月球表面固定一竖直光滑圆形轨道,在轨道内的最低点,放一可视为质点的小球,当给小球水平初速度v0时,小球刚好能在竖直面内做完整的圆周运动。已知圆形轨道半径为r,月球的半径为R 。若在月球表面上发射一颗环月卫星,求最小发射速度。
[新题导练]3.航天宇航员在月球表面完成了如下实验:如图所示,在月球表面固定一竖直光滑圆形轨道,在轨道内的最低点,放一可视为质点的小球,当给小球水平初速度v0时,小球刚好能在竖直面内做完整的圆周运动。已知圆形轨道半径为r,月球的半径为R 。若在月球表面上发射一颗环月卫星,求最小发射速度。
热点4 与万有引力定律相关的信息题
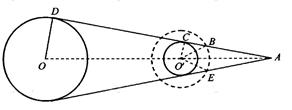 [真题4]我国发射的“嫦娥一号”探月卫星沿近似于圆形轨道绕月飞行。为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化。卫星将获得的信息持续用微波信号发回地球。设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R1,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r1,月球绕地球转动的周期为T。假定在卫星绕月运行的一个周期内卫星轨道平面与地月连心线共面,求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(用M、m、R、R1、r、r1和T表示,忽略月球绕地球转动对遮挡时间的影响)。
[真题4]我国发射的“嫦娥一号”探月卫星沿近似于圆形轨道绕月飞行。为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化。卫星将获得的信息持续用微波信号发回地球。设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R1,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r1,月球绕地球转动的周期为T。假定在卫星绕月运行的一个周期内卫星轨道平面与地月连心线共面,求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(用M、m、R、R1、r、r1和T表示,忽略月球绕地球转动对遮挡时间的影响)。
[解析] 如图所示:设O和 分别表示地球和月球的中心.在卫星轨道平面上,A是地月连心线
分别表示地球和月球的中心.在卫星轨道平面上,A是地月连心线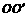 与地月球表面的公切线ACD的交点,D、C和B分别是该公切线与地球表面、月球表面和卫星轨道的交点.过A点在另一侧作地月球面的公切线,交卫星轨道于E点.卫星在圆弧
与地月球表面的公切线ACD的交点,D、C和B分别是该公切线与地球表面、月球表面和卫星轨道的交点.过A点在另一侧作地月球面的公切线,交卫星轨道于E点.卫星在圆弧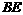 上运动时发出的信号被遮挡.
上运动时发出的信号被遮挡.
设探月卫星的质量为m0,万有引力常量为G,根据万有引力定律有: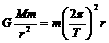 ①
① 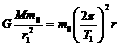 ②,②式中,T1表示探月卫星绕月球转动的周期.
②,②式中,T1表示探月卫星绕月球转动的周期.
由以上两式可得: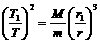 …………③
…………③
设卫星的微波信号被遮挡的时间为t,则由于卫星绕月球做匀速圆周运动,
应有: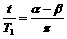 ④, 式中
④, 式中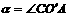 ,
,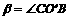 .
.
由几何关系得: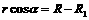 ⑤ ,
⑤ , 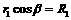 ⑥
⑥
由③④⑤⑥得: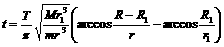 ⑦
⑦
[答案]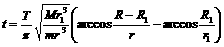
[名师指引] 解题的关键是要准确理解题中信息的含义,并找到信息与万有引力定律之间的结合点。
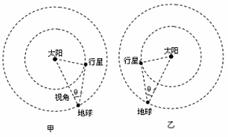 [新题导练]4.地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。地球的轨道半径为R=1.50×1011m,运转周期为T=3.16×107s。地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角)。当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,如图甲或图乙所示,该行星的最大视角θ=14.5°。求该行星的轨道半径和运转周期(sin14.5°=0.25,最终计算结果均保留两位有效数字)
[新题导练]4.地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动。地球的轨道半径为R=1.50×1011m,运转周期为T=3.16×107s。地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角)。当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期,如图甲或图乙所示,该行星的最大视角θ=14.5°。求该行星的轨道半径和运转周期(sin14.5°=0.25,最终计算结果均保留两位有效数字)
★抢分频道
限时基础训练卷
3.根据万有引力定律及向心力公式,可推导出线速度.角速度.周期随高度变化的关系,具体关系如下:
①由 得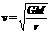 ,r越大,v越小;
,r越大,v越小;
②由 得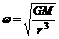 ,r越大,ω越小;
,r越大,ω越小;
③由 得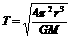 ,r越大,T越大.
,r越大,T越大.
|
[特别提醒]:卫星在变轨过程中,机械能并不守恒。轨道半径越大,运动的速度越小,但发射时所需要的能量却越多,即发射速度要越大。 |
[例3] (2009深圳外国语学校) “嫦娥一号”探月卫星以圆形轨道绕月飞行,卫星将获取的信息以微波信号发回地球,假设卫星绕月的轨道平面与地月连心线共面,各已知物理量如表中所示:
|
地球质量 |
月球质量 |
地球半径 |
月球半径 |
月球表面 重力加速度 |
月球绕地轨道半径 |
卫星绕月轨道半径 |
|
M |
m |
R |
R1 |
g1 |
r
|
r1 |
(1)嫦娥一号在奔月过程中受地球和月球引力相等时离月球面的高度为多少?
(2)嫦娥一号绕月球一周所用的时间为多少?
[解析](1)设卫星质量m′,由万有引力定律得:
卫星受地球和月球引力相等有: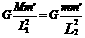
又因为:L1+L2=r , 卫星到月球表面的距离为:S=L2-R1
由上各式解得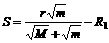
(2)由月球对卫星的万有引力提供向心力得: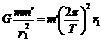
在月球表面有: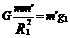
解得绕月球一周所用的时间为: 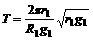
[答案](1)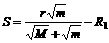 (2)
(2)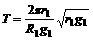
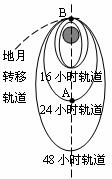 [例4]我国研制的“嫦娥一号”卫星于2007年10月24日18时由长征三甲运载火箭发射升空,星箭分离后在远地点做了一次变轨,进入到16小时轨道,然后分别在16小时、24小时(停泊轨道)、48小时轨道(调相轨道)轨道近地点,各进行了一次变轨,其中在调相轨道近地点变轨后,“嫦娥一号”卫星进入地月转移轨道正式奔月,下列说法中正确的是( )
[例4]我国研制的“嫦娥一号”卫星于2007年10月24日18时由长征三甲运载火箭发射升空,星箭分离后在远地点做了一次变轨,进入到16小时轨道,然后分别在16小时、24小时(停泊轨道)、48小时轨道(调相轨道)轨道近地点,各进行了一次变轨,其中在调相轨道近地点变轨后,“嫦娥一号”卫星进入地月转移轨道正式奔月,下列说法中正确的是( )
A.“嫦娥一号”由24小时轨道变为48小时轨道时应让其发动机在A点点火向后喷气
B.“嫦娥一号”由24小时轨道变为48小时轨道时应让其发动机在B点点火向后喷气
C.“嫦娥一号”沿24小时轨道在B点的速度大于沿24小时轨道在A点的速度
D.“嫦娥一号”沿48小时轨道在B点的加速度大于沿24小时轨道在B点的加速度
[解析] “嫦娥一号”由由24小时轨道变为48小时轨道应做离心运动,此时要增大速度,若选在A点点火,这样会使卫星进入另一个与A点相切的椭圆轨道,而不会进入预定的与B点相切的48小时轨道,因此要在B点点火,A错B对;“嫦娥一号”沿24小时椭圆轨道运动时,B点相当于近地点而A点相当于远地点,根据机械能守恒可知C选项正确。根据公式GMm/R2=ma可知“嫦娥一号”沿48小时轨道在B点的加速度等于沿24小时轨道在B点的加速度,故D错。
[答案]B、C
[规律总结] 在处理变轨问题时,一定要分清圆周轨道与椭圆轨道,弄清楚轨道切点上速度的关系,再根据机械能的变化分析卫星的运动情况。
考点4 万有引力与重力的关系、“黄金代换”关系
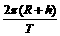
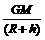
 赤道上空的同步轨道。关于成功定点后的“天链一号01星”,下列说法正确的是( )
赤道上空的同步轨道。关于成功定点后的“天链一号01星”,下列说法正确的是( )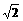 V1=11.2 km/s,使物体挣脱 引力束缚的最小发射速度。
V1=11.2 km/s,使物体挣脱 引力束缚的最小发射速度。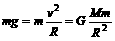 得
得 。这是人造地球卫星的最小 速度,也是人造地球卫星环绕地球运行的最
速度。
。这是人造地球卫星的最小 速度,也是人造地球卫星环绕地球运行的最
速度。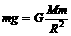 ,即地球表面处的重力加速度
,即地球表面处的重力加速度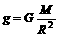 ;在距地表高度为h的高空处,万有引力引起的重力加速度为g',由牛顿第二定律可得:
;在距地表高度为h的高空处,万有引力引起的重力加速度为g',由牛顿第二定律可得: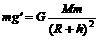 即:
。
即:
。