0 136700 136708 136714 136718 136724 136726 136730 136736 136738 136744 136750 136754 136756 136760 136766 136768 136774 136778 136780 136784 136786 136790 136792 136794 136795 136796 136798 136799 136800 136802 136804 136808 136810 136814 136816 136820 136826 136828 136834 136838 136840 136844 136850 136856 136858 136864 136868 136870 136876 136880 136886 136894 447348
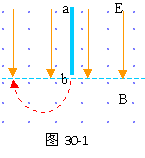 如图30-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。
如图30-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。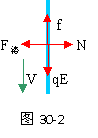 分析与解:(1)带电小球在沿杆向下运动时,
分析与解:(1)带电小球在沿杆向下运动时,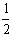 mVb2
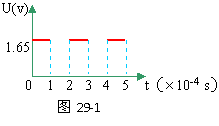
mVb2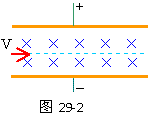 平行金属,板长1.4米,两板相距30厘米,两板间匀强磁场的B为1.3×10-3特斯拉,两板间所加电压随时间变化关系如29-1图所示。当t=0时,有一个a粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁场方向射入,如29-2图所示。不计a粒子的重力,求:该粒子能否穿过金属板间区域?若不能,打在何处?若能,则需多长时间?
(已知a粒子电量q=3.2×10-19库,质量m=6.64×10-27千克)
平行金属,板长1.4米,两板相距30厘米,两板间匀强磁场的B为1.3×10-3特斯拉,两板间所加电压随时间变化关系如29-1图所示。当t=0时,有一个a粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁场方向射入,如29-2图所示。不计a粒子的重力,求:该粒子能否穿过金属板间区域?若不能,打在何处?若能,则需多长时间?
(已知a粒子电量q=3.2×10-19库,质量m=6.64×10-27千克)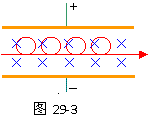 分析与解:在t=0到t=1×10-4秒时间内,两板间加有电压,a粒子受到电场力和洛仑兹力分别为:F=qu/d=q×1.56/0.3=5.2q
方向竖直向下
分析与解:在t=0到t=1×10-4秒时间内,两板间加有电压,a粒子受到电场力和洛仑兹力分别为:F=qu/d=q×1.56/0.3=5.2q
方向竖直向下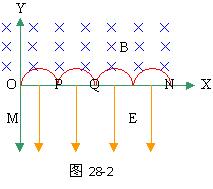 设释放点M的坐标为(0.-yO),在电场中由静
设释放点M的坐标为(0.-yO),在电场中由静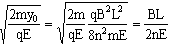
 粒子在磁场中做匀速圆周运动的半周期为t2,共n次,t2=πm/qB
粒子在磁场中做匀速圆周运动的半周期为t2,共n次,t2=πm/qB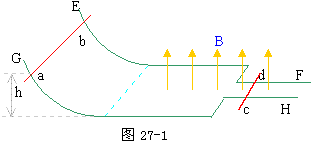 分析与解:ab下滑进入磁场后切割磁感线,在abcd电路中产生感应电流,ab、cd各受不同的磁场力作用而分别作变减速、变加速运动,电路中感应电流逐渐减小,当感应电流为零时,ab、cd不再受磁场力作用,各自以不同的速度匀速滑动。全过程中系统内机械能转化为电能再转化为内能,总能量守恒。
分析与解:ab下滑进入磁场后切割磁感线,在abcd电路中产生感应电流,ab、cd各受不同的磁场力作用而分别作变减速、变加速运动,电路中感应电流逐渐减小,当感应电流为零时,ab、cd不再受磁场力作用,各自以不同的速度匀速滑动。全过程中系统内机械能转化为电能再转化为内能,总能量守恒。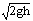 ,Vcd=(3/10)
,Vcd=(3/10)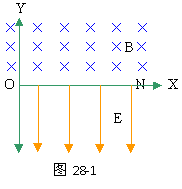 ④金属棒所受磁场力是系统的外力,且Fab≠Fcd时,合力不为零,故系统动量不守恒,只有当Lab=Lcd时,Fab=Fcd,方向相反,其合力为零时,系统动
④金属棒所受磁场力是系统的外力,且Fab≠Fcd时,合力不为零,故系统动量不守恒,只有当Lab=Lcd时,Fab=Fcd,方向相反,其合力为零时,系统动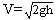 ,则安培力可表达为:
,则安培力可表达为: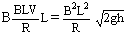 [2]
[2]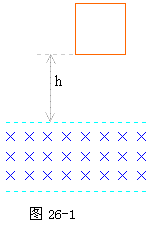 设导线横截面积为S,其质量为:m=4LSD [3]
设导线横截面积为S,其质量为:m=4LSD [3]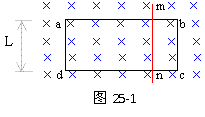 如图25-1所示为矩形的水平光滑导电轨道abcd,ab边和cd边的电阻均为5R0,ad边和bc边长均为L,ad边电阻为4R0,bc边电阻为2R0,整个轨道处于与轨道平面垂直的匀强磁场中,磁感强度为B。轨道上放有一根电阻为R0的金属杆mn,现让金属杆mn在平行轨道平面的未知拉力F作用下,从轨道右端以速率V匀速向左端滑动,设滑动中金属杆mn始终与ab、cd两边垂直,且与轨道接触良好。ab和cd边电阻分布均匀,求滑动中拉力F的最小牵引功率。
如图25-1所示为矩形的水平光滑导电轨道abcd,ab边和cd边的电阻均为5R0,ad边和bc边长均为L,ad边电阻为4R0,bc边电阻为2R0,整个轨道处于与轨道平面垂直的匀强磁场中,磁感强度为B。轨道上放有一根电阻为R0的金属杆mn,现让金属杆mn在平行轨道平面的未知拉力F作用下,从轨道右端以速率V匀速向左端滑动,设滑动中金属杆mn始终与ab、cd两边垂直,且与轨道接触良好。ab和cd边电阻分布均匀,求滑动中拉力F的最小牵引功率。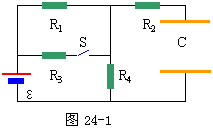 分析与解:(1)电键S闭合时,R1、R3并联与R4串联,(R2中没有电流通过)
分析与解:(1)电键S闭合时,R1、R3并联与R4串联,(R2中没有电流通过)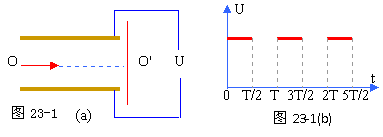 两平行金属板相距为d,加上如图23-1(b)所示的方波形电压,电压的最大值为U0,周期为T。现有一离子束,其中每个离子的质量为m,电量为q,从与两板等距处沿着与板平行的方向连续地射入两板间的电场中。设离子通过平行板所需的时间恰为 T(与电压变化周期相同),且所有离子都能通过两板间的空间打在右端的荧光屏上。试求:离子击中荧光屏上的位置的范围。(也就是与O‘点的最大距离与最小距离)。重力忽略不计。
两平行金属板相距为d,加上如图23-1(b)所示的方波形电压,电压的最大值为U0,周期为T。现有一离子束,其中每个离子的质量为m,电量为q,从与两板等距处沿着与板平行的方向连续地射入两板间的电场中。设离子通过平行板所需的时间恰为 T(与电压变化周期相同),且所有离子都能通过两板间的空间打在右端的荧光屏上。试求:离子击中荧光屏上的位置的范围。(也就是与O‘点的最大距离与最小距离)。重力忽略不计。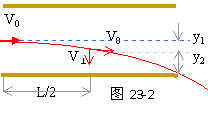 各个离子在电场中运动时,其水平分运动都是匀速直线运动,而经过电场所需时间都是T,但不同的离子进入电场的时刻不同,由于两极间电压变化,因此它们的侧向位移也会不同。
各个离子在电场中运动时,其水平分运动都是匀速直线运动,而经过电场所需时间都是T,但不同的离子进入电场的时刻不同,由于两极间电压变化,因此它们的侧向位移也会不同。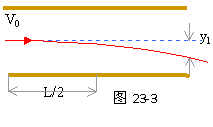 当离子在T=t/2,3/2T,5/2T……时刻进入电场
当离子在T=t/2,3/2T,5/2T……时刻进入电场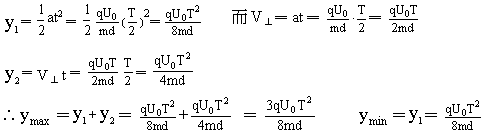
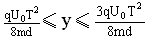
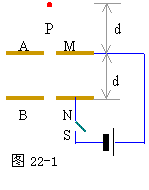 如图22-1所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有小孔M、N。今有一带电质点,自A板上方相距为d的P点由静止自由下落(P、M、N三点在同一竖直线上),空气阻力不计,到达N点时速度恰好为零,然后按原路径返回。若保持两板间的电压不变,则:
如图22-1所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有小孔M、N。今有一带电质点,自A板上方相距为d的P点由静止自由下落(P、M、N三点在同一竖直线上),空气阻力不计,到达N点时速度恰好为零,然后按原路径返回。若保持两板间的电压不变,则:
 。(1分)
。(1分)