0 136617 136625 136631 136635 136641 136643 136647 136653 136655 136661 136667 136671 136673 136677 136683 136685 136691 136695 136697 136701 136703 136707 136709 136711 136712 136713 136715 136716 136717 136719 136721 136725 136727 136731 136733 136737 136743 136745 136751 136755 136757 136761 136767 136773 136775 136781 136785 136787 136793 136797 136803 136811 447348
 如图所示,一个内外半径均可看作R=
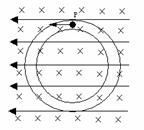
如图所示,一个内外半径均可看作R= 、光滑绝缘且竖直放置的细圆管,处于水平方向的匀强电场和匀强磁场内,电场与管道平面平行向左,磁场垂直管道平面向里。一个带正电的小球置于细圆管内,其所受电场力是重力的
、光滑绝缘且竖直放置的细圆管,处于水平方向的匀强电场和匀强磁场内,电场与管道平面平行向左,磁场垂直管道平面向里。一个带正电的小球置于细圆管内,其所受电场力是重力的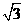 倍,现在最高点P给该小球一水平向左的初速
倍,现在最高点P给该小球一水平向左的初速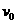 ,恰好使小球在细圆管内做完整的圆周运动。
,恰好使小球在细圆管内做完整的圆周运动。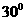 ,因为洛伦兹力不做功,故小球在合力方向上的M、N两点速度分别最大和最小。小球恰好做完整的圆周运动,说明在N点速度为零。
,因为洛伦兹力不做功,故小球在合力方向上的M、N两点速度分别最大和最小。小球恰好做完整的圆周运动,说明在N点速度为零。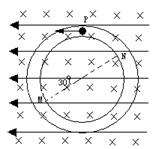 (1)
(1)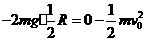 (2分)
(2分)
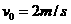 (1分)
(1分)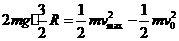 (3分)
(3分)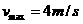 (1分)
(1分)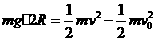 (1分)
(1分) 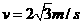 (1分)
(1分)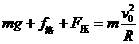 (1分)
(1分)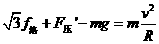 (1分)
(1分)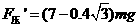 (1分)
(1分)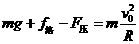 (1分)
(1分)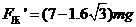 (1分)
(1分)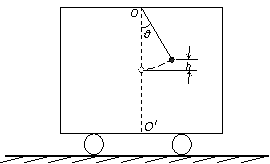 (2)当小球相对汽车静止时,细线偏移竖直方向的夹角(用反三角函数表示);
(2)当小球相对汽车静止时,细线偏移竖直方向的夹角(用反三角函数表示);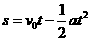 得
(2分)
得
(2分)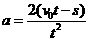 (2分)
(2分)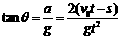 (2分)
(2分)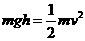 (1分)
(1分)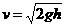 (1分)
(1分)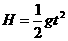 (1分)
(1分)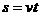 (1分)
(1分)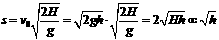 (2分)
(2分)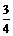 圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高, MN 是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.
圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高, MN 是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.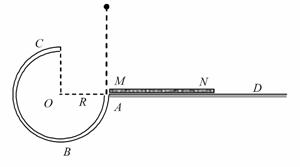
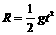 运动时间
运动时间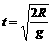 (2分)
(2分)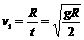 (1分)
(1分)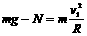 (1分)
(1分)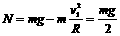 ,
(1分)
,
(1分)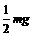 ,方向竖直向下. (1分)
,方向竖直向下. (1分)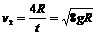 (2分)
(2分)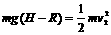 (2分)
(2分)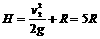 (2分)
(2分)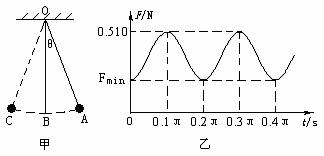 将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中O点为单摆的固定悬点,现将质量m=0.05㎏的小摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的A、C之间来回摆动,其中B点为运动中的最低位置。∠AOB=∠COB=θ(θ小于10°且是未知量)。;由计算机得到的细线对摆球的拉力大小F随时间t变化的曲线如图乙所示,且图中t=0时刻为摆球从A点开始运动的时刻。g取10m/s2,试根据力学规律和题中所给的信息,求:
将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中O点为单摆的固定悬点,现将质量m=0.05㎏的小摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的A、C之间来回摆动,其中B点为运动中的最低位置。∠AOB=∠COB=θ(θ小于10°且是未知量)。;由计算机得到的细线对摆球的拉力大小F随时间t变化的曲线如图乙所示,且图中t=0时刻为摆球从A点开始运动的时刻。g取10m/s2,试根据力学规律和题中所给的信息,求: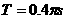 (2分)
(2分)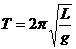 ,得
,得 (3分)
(3分)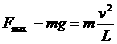 (3分)
(3分)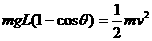 (3分)
(3分)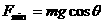 (2分)
(2分) (2分)
(2分)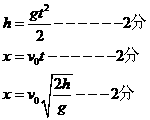 已知h=300 m,v0=30 m/s,当水流沿水平方向射出时,在水平地面上落点最远,由平抛规律:
已知h=300 m,v0=30 m/s,当水流沿水平方向射出时,在水平地面上落点最远,由平抛规律: 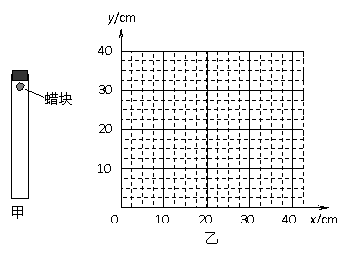 如图甲所示,在一端封闭、长约lm的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1s上升的距离都是10cm,玻璃管向右匀加速平移,每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点.
如图甲所示,在一端封闭、长约lm的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1s上升的距离都是10cm,玻璃管向右匀加速平移,每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点.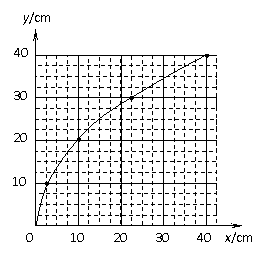
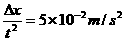 (2分)
(2分)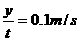 (1分)
(1分) (2分)
(2分)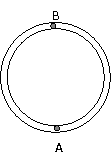 一内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径略小于细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为v0.设A球运动到最低点时,B球恰好运动到最高点,重力加速度用g表示.
一内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径略小于细管内径相同的小球(可视为质点).A球的质量为m1,B球的质量为m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为v0.设A球运动到最低点时,B球恰好运动到最高点,重力加速度用g表示.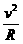 (1分)
(1分)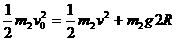 (1分)
(1分)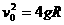 (1分)
(1分) (1分)
(1分)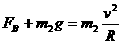 (1分)
(1分)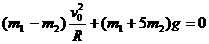 (1分)
(1分)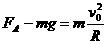
 (1分)
(1分)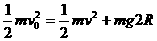 (1分)
(1分)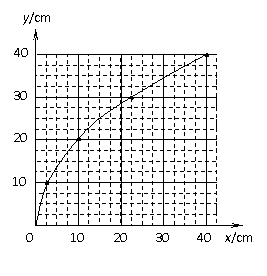 (1)请在图乙中画出蜡块4s内的轨迹;
(1)请在图乙中画出蜡块4s内的轨迹;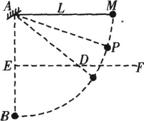 (3)保持小钉D的位置不变,让小球从图示的P点静止释放,当小球运动到最低点时,若细线刚好达到最大张力而断开,最后小球运动的轨迹经过B点.试求细线能承受的最大张力T.
(3)保持小钉D的位置不变,让小球从图示的P点静止释放,当小球运动到最低点时,若细线刚好达到最大张力而断开,最后小球运动的轨迹经过B点.试求细线能承受的最大张力T.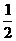 mv2
T1-mg=m
mv2
T1-mg=m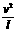
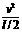 ∴T1=3mg T2=5mg
∴T1=3mg T2=5mg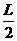 -r)=
-r)=
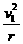 ②
②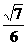 L ⑤
L ⑤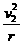 ⑥ 以后小球做平抛运动过B点,在水平方向有x=v2t ⑦
⑥ 以后小球做平抛运动过B点,在水平方向有x=v2t ⑦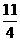 mg
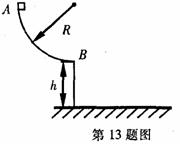
mg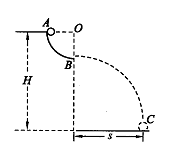 54、如图所示,位于竖直平面内有1/4圆弧的光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H。当把质量为m的钢球从A点静止释放,最后落在了水平地面的C点处。若本地的重力加速度为g,且不计空气阻力。试计算:
54、如图所示,位于竖直平面内有1/4圆弧的光滑轨道,半径为R,OB沿竖直方向,圆弧轨道上端A点距地面高度为H。当把质量为m的钢球从A点静止释放,最后落在了水平地面的C点处。若本地的重力加速度为g,且不计空气阻力。试计算: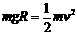
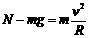
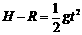
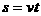
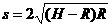
 (1)小滑块沿圆弧轨道运动过程中所受摩擦力做的功;
(1)小滑块沿圆弧轨道运动过程中所受摩擦力做的功; m/s
m/s